케플러 2 법칙: 면적 속도 일정 법칙
왜 2법칙부터 설명하냐면 2법칙부터 설명하는게 편하므로
각운동량이 L=rXp 이므로 각운동량을 시간에 대해 미분하면

이다.
그런데 p=mv니까 앞의 항의 v X p=v X v *m라고 쓸 수 있는데 v끼리 이루는 각은 0도니까 벡터곱은 0이 되므로 무시할 수 있다.
따라서

라고 쓸 수 있다.
그런데 r은 지구 중심-우주선 벡터고, 힘은 중심력(지구의 중력)인데 이 두 벡터는 평행하므로 값이 0이다.
뭔 뜻이냐면, 궤도를 그리는 우주선은 어디서나 일정한 각운동량을 가진다는 거다(미분값이 0이니까 각운동량은 상수)
이제 이게 면적하고 뭔 관계가 있냐를 증명할것이다.

각운동량 L=mrv인데 v를 r*θ의 시간에 대한 미분으로도 쓸 수 있으므로(호의 길이)

이렇게 쓸 수도 있다
그럼 저 위에서 직각삼각형의 면적(A)은 (1/2)*(dθ/dt)*r^2라고 할 수 있으므로

이렇게 쓸 수 있다
이게 뭔 의미냐면 일정시간동안(dt)쓸고 지나간 면적(dA)는 일정하다(L,m은 상수이므로)라는 것이다.: 케플러 2 법칙
예시를 들어 보겠다

각운동량: 1(질량)*704.8*(2720+600)=2,339,936(단위는 신경안씀)

각운동량: 1* 2313.6*(411.5+600)=2,340,206으로 거의 비슷하다.
케플러 1 법칙: 타원 궤도 법칙
여기서부터는 꽤 어려워질 것이다.
극좌표계에서 가속도는 위키피디아 참조:https://en.wikipedia.org/wiki/Polar_coordinate_system#Vector_calculus
간단히 말해서 극좌표계에서 중심 방향 가속도는

고, Prograde 방향 가속도는

라는 것만 기억하면 된다.
궤도를 돌고 있을때 지구 중심 방향 힘은

(f(r)은 거리에 따른 중력의 세기 함수)
Prograde 방향 힘은

(가해지는 힘이 없으니까)
그런데,

이 식은
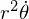
이 식 미분하면 나온다.
앞에서 케플러 2 법칙 증명할 때
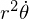
가 상수라는 것도 알게 되었고 단위 질량당 각운동량이므로 l(소문자 L)이라고 부를것이다.
이제 어떤 궤도가 나오는지에 대해 알아볼거다
먼저 지구 중심으로부터의 거리 r을 1/u 라고 바꾸겠다
그럼 위의 식들을 잘 이용해서 r=1/u를 전개하면

라고 할 수 있다
이걸 한번 더 미분해 보면

이렇게 된다(연쇄법칙 사용: https://en.wikipedia.org/wiki/Chain_rule )
이걸 위의 지구 중심 방향 힘에 대입하고 식을 정리하면

이렇게 된다.
이제 역제곱 법칙 힘이 가해지는 곳에서의 궤도를 구할거다
잘 알듯이 중력은 GMm/r^2의 세기로 작용한다.
일단 이 GMm을 k라고 치환해서 f(r)=-k/r이라고 해 놓겠다
그럼

이고 이건 조화 진동자의 미분 방정식인데 의미는 진자나 용수철처럼 주기를 갖는다는 뜻이다
자세히 알 필요는 없어서 대충 넘어가겠는데, 이건 비슷하게 주기를 갖는 함수인 코사인 함수로 풀 수 있다

이렇게 풀 수 있다
다시 정리하면

이렇게 되는데 이게 뭐냐면 극좌표계에서의 타원 방정식이다
타원의 방정식(극좌표):

(유도는 귀찮으므로 생략) ε(입실론)은 이심율이고 a는 장반경이다.

참고

이심률이 0이면 원궤도

이심율이 0<e<1이면 타원궤도

이심율이 1이면 포물선 궤도(탈출궤도)

이심율이 1 이상이면 쌍곡선 궤도
이 궤도들은 원뿔곡선인데 원뿔을 잘랐을 때 생길 수 있는 단면적이 이 모양중 하나로 나오기 때문이다.

이제 어떤 궤도를 갈 때 필요한 델타 V를 잘 계산할 수 있다(아직은 좀 불편하지만... Porkchop Plot글도 쓰고싶다.)
케플러 3법칙: 조화 법칙
이거 증명은 생각보다 쉽다.

이다. (케플러 2 법칙)
이걸 전체 궤도 주기에 대해 적분하면

타원의 넓이는 pi*a*b(원주율*긴반지름*짧은반지름)이므로 위 식을 잘 정리하면

양변을 제곱하면


이고

이므로(알파는 타원의 통경, 통경: 초점에서 장반경에 수직한 선이 타원과 만나는 점까지의 거리)
조화의 법칙이 증명된다.
타 커뮤니티에 쓴 거 여기에 백업한거다.
대부분 Fowles해석역학 책을 참고했다.
혹시 위에 점 찍는 게 뭔지 궁금하다면 뉴턴식 표기법으로 시간에 대한 미분을 나타낸 것이다.
'Physics > 고전역학' 카테고리의 다른 글
| 로켓방정식 (0) | 2021.01.22 |
|---|---|
| Kerbal Space Program으로 배우는 궤도역학 -궤도 경사각, 2입자 운동, 제한된 3입자 문제 (1) | 2021.01.21 |
| Kerbal Space Program으로 배우는 궤도역학 -궤도 에너지 (0) | 2021.01.21 |



댓글