궤도 경사각

궤도의 다른 조건은 유지하고 궤도 경사각만 바꾸고 싶다고 하면 위처럼 경사각을 바꾸기 전과 후의 속도 벡터의 크기는 동일할 것이므로
저렇게 이등변 삼각형을 만들 거다.
그럼 저 이등변 삼각형의 짧은 변의 길이(=델타 V)를 구하면 됨
그럼 저 짧은 변의 길이는 어떻게 구하냐면, 코사인 법칙을 이용하면 된다.
(코사인 법칙: https://ko.wikipedia.org/wiki/%EC%BD%94%EC%82%AC%EC%9D%B8_%EB%B2%95%EC%B9%99)

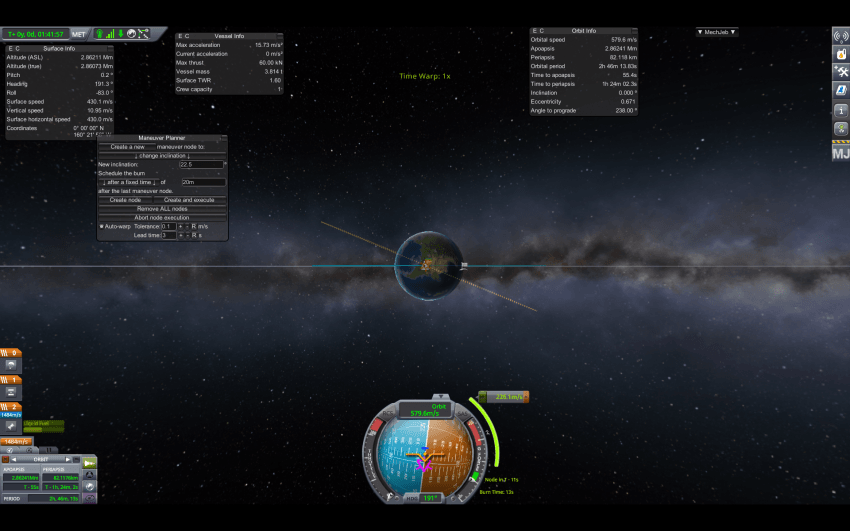
계산해보면 v^2= 579.6^2+579.6^2-2*579.6*579.6*cos(22.5)=51143, v=226m/s 로 KSP에서 확인한 것과 정확히 일치함
속도벡터가 작을 때 궤도경사각을 바꾸면 이득이니까 궤도경사각은 Ap에서 바꾸는 게 유리하다.
2입자 운동
ksp에서는 뮌이 커빈 주위를 돌고, 커빈이 태양 주위를 도는데
명왕성하고 카론같이 질량이 상당히 비슷한 것들끼리 돌면 둘의 질량 중심을 기준으로 돈다고 보는 게 더 정확하다
그래서 질량이 비슷한 두 물체가 도는 중이면 케플러 법칙이 아니라 2입자 운동으로 계산해야 된다.
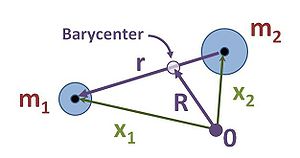
이렇게 공통 질량 중심을 돈다는 걸 알 수 있다.
별로 중요하진 않으니까 자세한 정보는:https://en.wikipedia.org/wiki/Two-body_problem
실험해보고 싶으면 이 사이트에서:https://evgenii.com/blog/two-body-problem-simulator/
제한된 3입자 문제: Principia 모드
궤도를 도는 물체의 질량이 작으면, 케플러 궤도는 거의 맞는데, 궤도를 도는 물체의 질량이 크면 케플러 법칙은 잘 안맞기 때문에 2입자계 운동으로 풀어야된다.
그런데, 2입자계 운동에서 질량이 작은 물체(인공위성 같은거)를 놓으면 어떻게 되는지를 알고 싶을거임 3번째 물체의 질량을 무시할 수 있는 수준이라서 제한된 3입자 문제라고 이름이 붙는다
이 문제는 미분방정식 형태로 운동 방정식이 나오는데 일반해를 구하는 게 불가능해서 수치해석으로 풀어야된다.

이렇게 입자들이 있고 이 입자들이 회전하고 있다고 생각하면 된다.
2입자 운동으로 볼 때 원점이 질량 중심이고, 원점-M1을 x축으로 회전하는 좌표계라고 보면 된다.
그럼 작은 질량 m이 받는 중력은

(r1/r1, r2/r2는 위치벡터)
이게 실제 작용하는 힘인데, 여기서는 회전하는 좌표계에서 보기 때문에 비관성력(구심 가속도, 코리올리 가속도)을 고려해야 된다.
회전좌표계에서의 비관성력: https://en.wikipedia.org/wiki/Rotating_reference_frame
이걸 xy좌표계로 옮기면 되는데 궁금하면 위의 위키피디아에서 코리올리 힘이나 구심 가속도 링크 참조
그래서 잘 계산하면
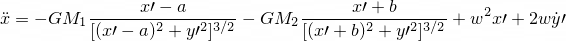

이런 두 개의 미분 방정식이 나오는데
이걸 룽게-쿠타법같은 걸로 컴퓨터로 풀면 위치와 속도를 알 수 있다
룽게-쿠타법: https://en.wikipedia.org/wiki/Runge%E2%80%93Kutta_methods
이제 위치 에너지를 구해봐서 라그랑주점에 대해 설명하겠다
위 식을 잘 적분해서 위치 에너지를 구해보면(정확히는 유효 위치 에너지)

이렇게 되는데 이 함수를 그리면 대충 이렇게 나옴

여기서 저 곡면 위의 점의 z축 좌표가 그 위치에서의 위치 에너지이다
1. 점의 좌표가 달이나 지구에 가까이 있어서 위치 에너지가 -무한대면 케플러 궤도를 돈다고 할 수 있다
2. 점의 좌표가 지구-달 시스템 밖에 있어서 위치 에너지가 -무한대면 : 탈출궤도
3. 위치 에너지의 변화량(∇위치 에너지함수)=0인 점: 라그랑주점
1. L1, L2, L3: 불안정한 평형점: 이 점을 중심으로 리사주 궤도를 그리면서 돔
2. L4, L5: 안정한 평형점: 코리올리 힘과 위치 에너지가 균형을 이뤄서 이 점을 중심으로 도는 궤도가 만들어짐
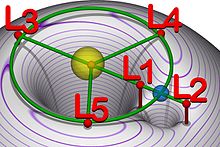
위치


L3, 지구 반대편에 달이 있음(지구-달 질량중심 좌표계에서 본 것임)
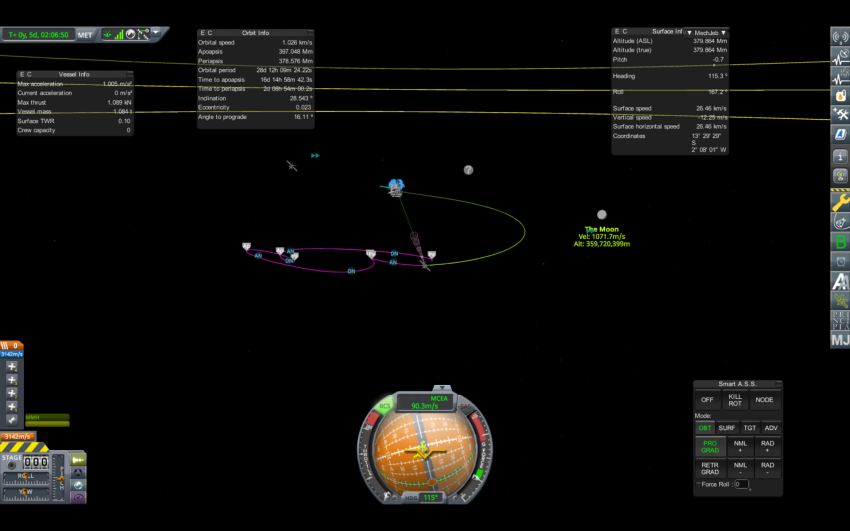

L4, 지구-달과의 각도가 60도인 지점

L2, 많이 불안정함
이 글 또한 백업용으로 쓰는 것이다. Fowles 책을 참조하였다.
'Physics > 고전역학' 카테고리의 다른 글
| 로켓방정식 (0) | 2021.01.22 |
|---|---|
| Kerbal Space Program으로 배우는 궤도역학 -궤도 에너지 (0) | 2021.01.21 |
| Kerbal Space Program으로 설명하는 궤도역학 -케플러 3 법칙 (0) | 2021.01.21 |


댓글