블랙홀 시뮬레이션 - 1. 일반상대론 설명

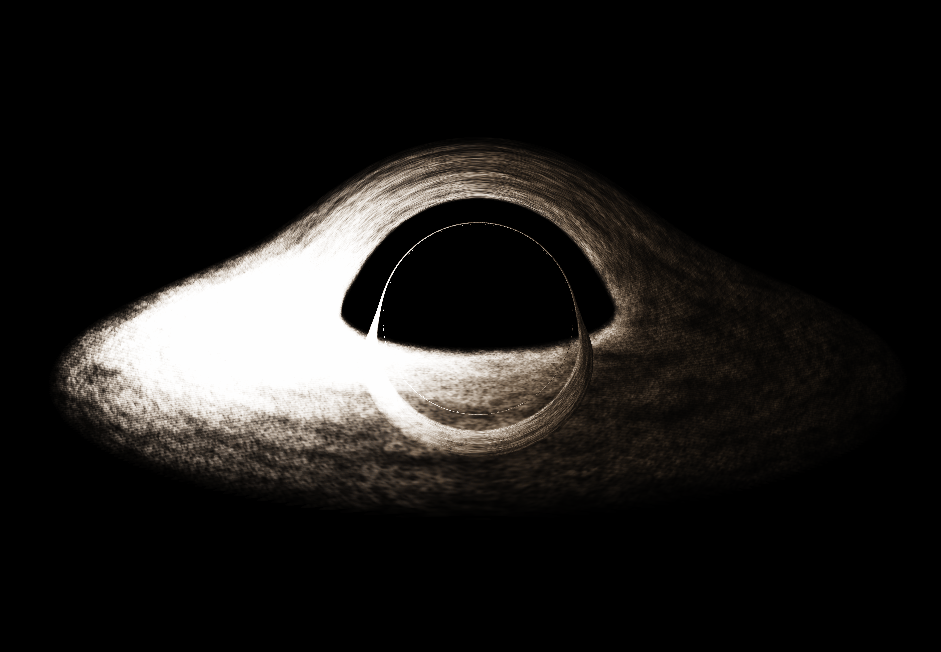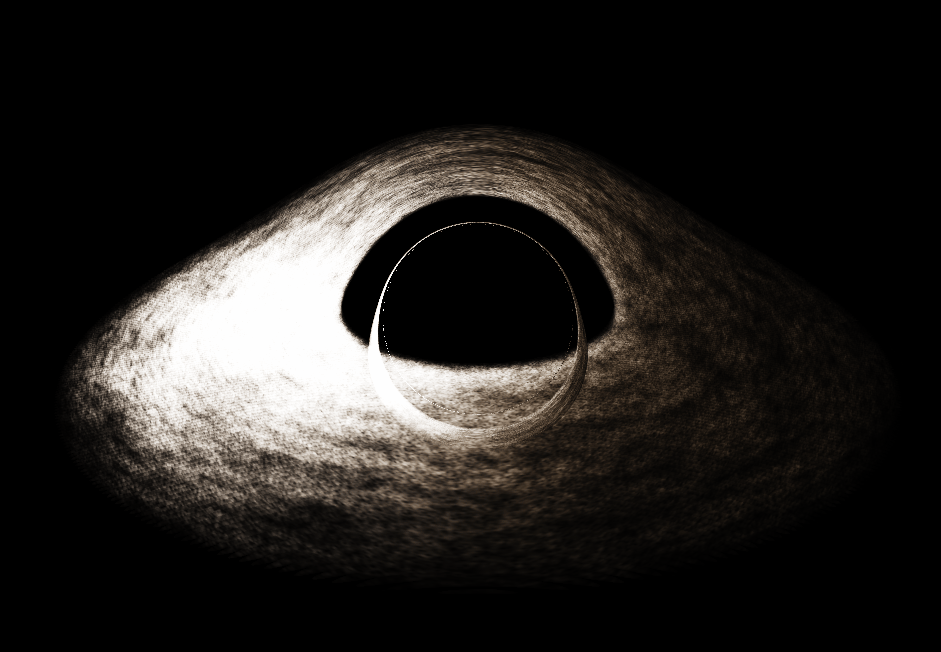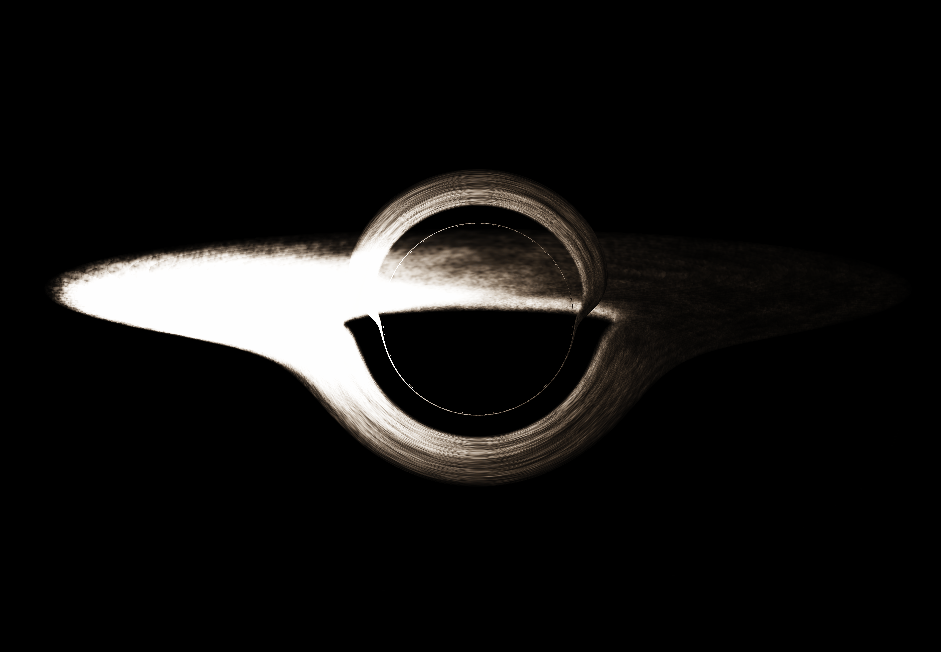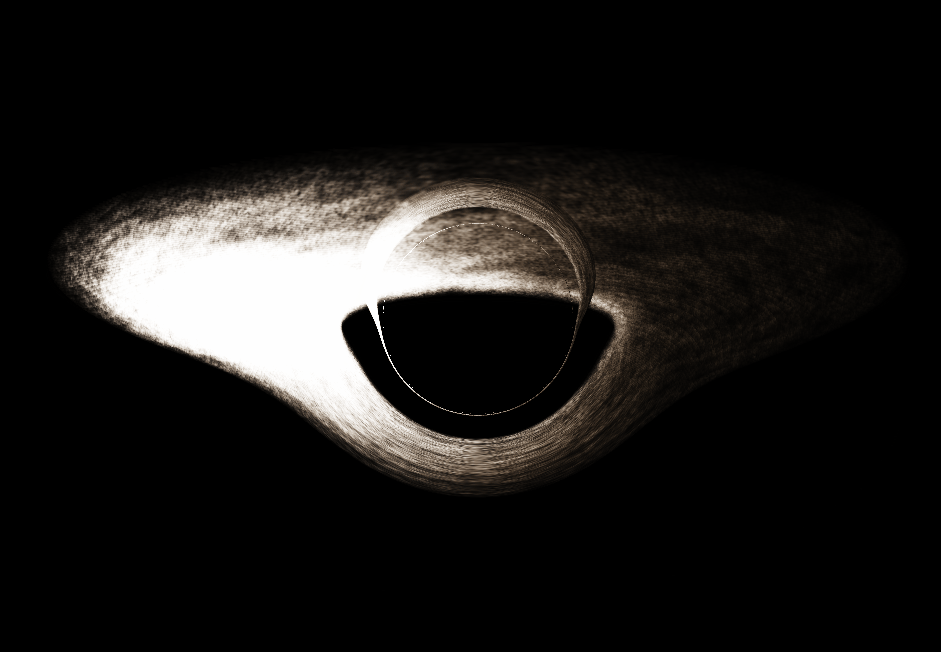
블랙홀 시뮬레이션을 만들었음.

 

작년에 학교에서 일반상대론을 배웠는데 이걸 가지고 뭔가 재밌는 짓을 하고 싶었음. 슈바르츠실트 블랙홀 정도면 쉽게 시뮬레이션을 만들 수 있을 것 같아 이렇게 블랙홀 시뮬레이션을 만들게 됨.

 

시뮬레이션을 어떻게 만들었는지 이해하기 위해서는 간단한 일반상대론과 컴공과 그래픽스 수업에서는 언급만 하고 넘어가는 주제인 레이 트레이싱에 대해 알아야 함. 일반상대론과 컴퓨터 그래픽스같이 복잡한 주제들을 이 글 하나에 다 적기에는 글을 읽는 사람의 기억력 여백이 부족할 것 같으므로 이번 글에는 일반상대론 이야기만 적도록 하겠음.

 

작년에 배웠던 거라 잊어버리기도 했고, 이 주제에 대해 그렇게 잘 아는 편도 아니어서 더 자세한 정보를 원한다면 다른 자료 참고 바람. 일단, 기본적인 물리학 지식(미적분, 벡터 해석, 라그랑주 역학)에 대한 지식이 있다고 가정하고 글을 쓸 것임. 

 

일단 코드는 이쪽 참고 바람 -> github: https://github.com/hydrogendeuteride/BlackHoleRayTracer

 

주의: 글이 수학적, 물리적으로 부족할 수 있으므로 틀렸다면 알려주기 바람.

 

텐서, 메트릭, 지오데식?

일단 블랙홀이 수학적으로 어떻게 표현될 수 있는지 알기 위해 텐서, 메트릭, 지오데식 등의 미분기하학에 대해 간단히 설명해보겠음.

 

텐서

어떤 벡터와 공변 벡터를 내적하면 스칼라가 나옴.

\[
\begin{bmatrix}
x & y & z
\end{bmatrix}
\begin{bmatrix}
a \\
b \\
c
\end{bmatrix}
 = x_i a^i\]

이런 식으로 나타낼 수 있음. 아인슈타인 표기법으로 합 기호는 삭제함

이 때 공변 벡터를 linear functional이나 one-form 라고 부르기도 함.

 

 만약 2개의 벡터를 받아 스칼라가 나오는 functional이 있다면 (0 2)텐서라고 함. 반대로 공변벡터를 받아서 스칼라가 나온다면 (2 0)텐서일 거고. 아주 간단히 하자면, 텐서는 벡터를 인자로 받는 함수라고 보면 됨.

 

텐서를 사용하는 이유는 물리 법칙이 공간 이동에 대해 불변해야 하기 때문임.

index lowering나 텐서곱 등은 이 글에서는 필요가 없으므로 따로 설명하지는 않겠음.

이 블로그에서 설명 잘해놨음: https://elementary-physics.tistory.com/155

 

메트릭 텐서

두 사건(=manifold 위의 두 점) 간의 거리를 잴 때 정의하는 텐서가 메트릭 텐서임.

 

3차원에서의 점 간의 거리는 $ds^2 = dx^2 + dy^2 + dz^2$라고 적을 수 있고, 시간축이 들어가는 4차원 특수 상대론에서는 두 사건 간의 거리 $ds^2 = -dt^2 + dx^2 + dy^2 + dz^2$라고 적을 수 있음. 기존의 거리 식에 시간 축 방향으로 한 개의 축이 더 늘어났을 뿐임. 간단히 하자면 두 벡터를 내적한 값을 우리가 보통 거리라고 부르는데, 이 때 메트릭 텐서가 내적을 정의해줌.

 

특수상대성이론에서 거리를 재는 방법인 민코프스키 메트릭:

\[
\eta_{\mu \nu} = 
\begin{pmatrix}
-1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 
\end{pmatrix}
\]

 

이 텐서는 벡터를 받아서 평평한 시공간에서의 거리를 알 수 있게 해 줌.

\[
ds^2 = \eta_{\mu \nu} dx^{\mu} dx^{\nu}
\]

이렇게(여기서 $dx$는 두 점 사이의 좌표 변화량)

 

이 때

$ds^2 > 0$ 이면 spacelike

$ds^2 = 0$ 이면 lightlike

$ds^2 < 0$ 이면 timelike

라고 함.

위의 민코프스키 다이어그램에서 회색 부분이 도달할 수 있는 timelike 공간, 회색과 흔색의 경계선이 lightlike worldline, 흔색 공간이 spacelike 공간임.

 

그런데 중간에 뭔가 무거운 것(ex. 중성자별) 때문에 공간이 휘어진다면 거리를 어떻게 재야 할까?

 

지오데식

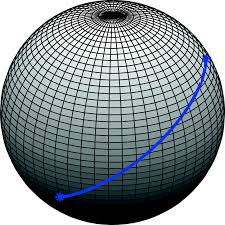
어떤 곡면 위에 있는 어떤 점에서 다른 점으로 이동할 때 최소 거리 곡선을 geodesic라고 함. 위 그림처럼 구 위에서의 최단 경로는 구를 잘랐을 때 가장 넓은 단면적이 나오는 궤적이 최소 거리 곡선이고 geodesic임.

 

아인슈타인 장 방정식에 따르면 질량이 시공간의 곡률을 만든다는 것을 알 수 있는데, 광자는 직선으로 이동하므로, 빛이 질량에 의해 휘어진다는 것을 알 수 있음. 이 때 빛은 최단 거리를 따라 이동하는데 이 때 $ds^2 = 0$으로 null geodesic라고도 함.

 

\[
G_{\mu \nu} + \Lambda g_{\mu \nu} = \frac{8 \pi G}{c^4} T_{\mu \nu}
\] 

아인슈타인 장 방정식은 이렇게 생겼는데, $G_{\mu \nu}$는 아인슈타인 텐서로 시공간의 곡률을 의미하고 $T_{\mu \nu}$는 스트레스-에너지 텐서로 에너지와 운동량의 분포를 나타냄. 아인슈타인 장 방정식의 의미는 에너지와 운동량으로 시공간이 휜다는 것을 의미함. 이 방정식으로 슈바르츠실트 블랙홀의 메트릭을 얻어낼 수 있지만, 지금 이 글도 4/18일부터 7/17일까지 세달동안 쓰고 있는데 그것도 쓰면 세달은 더 써야돼지 않을까?

 

그럼 이 때 geodesic equation은 어떻게 구할 수 있을까?

 

경로의 최소화에서 눈치 챈 사람도 있겠지만, 이 문제는 변분법을 통해 풀 수 있음.

그러면 빛의 이동 경로를 최소화 해 보자.

 

\[
S=\int\mathrm{d}s=\int{\frac{\mathrm{d}s}{\mathrm{d}\lambda}}\,\mathrm{d}\lambda=\int{\sqrt{\left({\frac{\mathrm{d}s}{\mathrm{d}\lambda}}\right)^{2}}}\,\mathrm{d}\lambda
\]

여기서 S는 액션이라고 하고 라그랑지안을 경로로 적분한 값임.

 

따라서 라그랑지안은

\[
L= \sqrt{\left(\frac{ds}{d\lambda}\right)^2} = \sqrt{-g_{\mu\nu} \frac{dx^{\mu}}{d\lambda}\frac{dx^{\nu}}{d\lambda}}
\]

 

라그랑지안을 오일러-라그랑주 방정식

\[
\frac{\partial L}{\partial x^{\mu}} - \frac{d}{d\lambda} \left( \frac{\partial L}{\partial \dot{x}^{\mu}} \right) = 0
\]

에 넣어 지오데식 방정식을 구할 수 있는데(여기서는 우변을 제곱해서 라그랑지안 미분을 계산하기 쉽게 할 수 있음):

 \[
\frac{d^2 x^\mu}{d \lambda^2} + \Gamma^\mu_{\rho \sigma} \frac{dx^\rho}{d \lambda} \frac{dx^\sigma}{d \lambda} = 0
\]

다음과 같이 나타남. 이 때 $\Gamma$는 크리스토펠 기호로 $ \Gamma^\mu_{\rho \sigma}  = \frac{1}{2} g^{\mu \nu} \left( \partial_\rho g_{\sigma \nu} + \partial_\sigma g_{\rho \nu} - \partial_\nu g_{\rho \sigma} \right) $ 으로 쓸 수 있음.

 

그럼 예시로 일단 평평한 시공간부터 한 번 지오데식 방정식을 구해보자.

 \[
L = -\dot t^2 + \dot x^2 + \dot y^2 + \dot z^2
\]

이고 오일러-라그랑주 방정식에 넣어 보면, $ x( \lambda) = a \lambda + b $형태의 해를 얻을 수 있고 이는 빛이 직진한다는 것을 의미함.

 

슈바르츠실트 메트릭

이제 슈바르츠실트 메트릭에 대해 지오데식 방정식을 구하면 빛이 어떤 경로로 이동하는지 알 수 있음.

 \[
ds^2 = - \left( 1 - \frac{2GM}{r} \right) dt^2 + \left( 1 - \frac{2GM}{r} \right)^{-1} dr^2 + r^2 \left( d\theta^2 + \sin^2 \theta \, d\phi^2 \right)
\]

여기서 $2GM$은 블랙홀의 반지름인데, 귀찮으니 그냥 1로 하자.

나중에 복잡해지지만 지금 간단하니 좋았쓰!!

여기서 $ r^2 \left( d\theta^2 + \sin^2 \theta \, d\phi^2 \right) $이 항은  구면 대칭성을 나타내므로 간단히 $r^2 d\Omega^2$로 써도 됨. 따라서

\[
ds^2 = - \left( 1 - \frac{1}{r} \right) dt^2 + \left( 1 - \frac{1}{r} \right)^{-1} dr^2 + r^2 d\Omega^2
\]

로 단순화할 수 있음.

 

라그랑지안을 구하면

\[
L = - \left( 1 - \frac{1}{r} \right) \dot t^2 + \left( 1 - \frac{1}{r} \right)^{-1} \dot r^2 + r^2 \dot \Omega^2
\]

 

이 라그랑지안을 오일러-라그랑주 방정식에 넣어보자. 일단 시간 좌표 $t$부터:

\[
\frac{\partial L}{\partial t} - \frac{d}{d\lambda}\frac{\partial L}{\partial \dot t} = \frac{d}{d\lambda}\left[\left(1-  \frac{1}{r}\right)\dot t\right] = 0
\]

그런데 여기서 알 수 있는 점이 있음. 시간 이동 대칭성에 의하면 라그랑지안이 시간에 대해 변하지 않으면 에너지가 보존됨. 따라서

\[
E = \left(1-  \frac{1}{r}\right)\dot t
\]

로 쓸 수 있음. 

 

이제 $\Omega$에 대해 같은 일을 해 보자.

\[
\frac{\partial L}{\partial \Omega} - \frac{d}{d\lambda}\frac{\partial L}{\partial \dot \Omega} = \frac{d}{d\lambda} \left(2 r^2 \dot \Omega \right) = 0
\]

회전에 대해 라그랑지안이 불변이므로 각운동량이 보존되고, 각운동량 $h=r^{2}\dot\Omega$ 라고 할 수 있음.

 

그럼 라그랑지안을 다시 써보면:

\[
L = \left( 1 - \frac{1}{r} \right)^{-1} (\dot r^2 - E^2) + \frac{h^2}{r^2}
\]

lightlike curve($ds^2 = 0$)를 구해야 빛의 움직임을 알 수 있으므로 
\[
L = \left( 1 - \frac{1}{r} \right)^{-1} (\dot r^2 - E^2) + \frac{h^2}{r^2} = 0
\]

그러면 이제 라그랑지안을 이용해서 유효 퍼텐셜을 구할 수 있음. 빛의 경우 $ds^2 = 0$이므로 좌변의 라그랑지안을 0으로 둘 수 있음.

\[
\left( 1 - \frac{1}{r} \right)^{-1} (\dot r^2 - E^2) + \frac{h^2}{r^2} = 0
\]

위치에 의해 결정되는 항만 우변으로 빼 주면

\[
V^2(r) = \dot r^2 - E^2 = \left( 1 - \frac{1}{r} \right)\frac{h^2}{r^2}
\]

그러면 

\[
\left(\frac{dr}{d\tau}\right)^2 = E^2 - V^2(r)
\]

양변을 $\tau$로 미분하면

\[
2 \left(\frac{dr}{d\tau}\right) \left(\frac{d^2r}{d\tau^2}\right) = - \frac{V^2(r)}{dr}\frac{dr}{d\tau}
\]

양변을 적절히 정리해주면

\[
\frac{d^2r}{d\tau^2} = - \frac{1}{2}\frac{d}{dr}V^2(r) = \frac{h^2}{r^3} - \frac{3}{2}\frac{h^2}{r^4}
\]

이 때 $-\frac{h^2}{r^3}$항은 고전역학에서의 원심력에 해당하는 항임. 따라서, 이 항은 비관성 좌표계에서는 사용되겠지만, . 따라서 이번에는 사용하지 않을 것임.

 

정리하면, 다음과 같은 식을 얻음.

\[
F(r) = \frac{d^2r}{d\tau^2} =  - \frac{3}{2}\frac{h^2}{r^4}
\]

 

이제 이 식으로 상대론적 레이 트레이싱을 해 보자(는 다음 글을 보자)

 

참고 자료:

Schutz, A First Course in General Relativity

https://en.wikipedia.org/wiki/Schwarzschild_geodesics

Schwarzschild geodesics - Wikipedia

https://flannelhead.github.io/posts/2016-03-06-photons-and-black-holes.html

flannelhead's lab - Photons and black holes