현재 개발된 NTR(Nuclear Thermal Rocket)들은 대부분 최대 900초 정도의 비추력과 대략 25~30톤 정도의 추력을 가짐. 이 정도면 호만전이궤도를 따라 화성 왕복은 충분하겠지만(대충 화성까지 5km/s dV, 복귀할 때 공력 제동을 사용한다면 3~4km/s 정도로 잡으면 질량비가 e = 2.718 정도로도 가능) 화성까지 100일 내로 빠르게 가야한다거나 화성을 넘어 소행성대나 수성으로 진출하기 위해서는 더 높은 성능의 엔진이 필요함.
제작된 적이 있는 엔진으로만 비교한다면 이온 엔진은 비추력이 NTR보다 최소 3배 이상 우수하지만 추력이 지나치게 약함. 이온 엔진으로 항해하는 우주선은 충분히 빠르게 가속할 수 없음.
Pulsed NTR은 원자로를 펄스로 작동시켜서 추력과 비추력 모두 증가시킬 수 있음.
추력을 증가시키는 법
로켓 엔진의 일률 P는 $P=\frac{\dot{m}_e v_e^2}{2}$ 로 쓸 수 있음. ($\dot{m}_e$는 질량 흐름, $v_e$는 배기 속력)
로켓 엔진의 추력 F는 $F = \dot{m}_e v_e$임.
로켓 엔진의 추력을 n배 증가시키고 싶다면 어떻게 될지 알아보겠음.
$F = n \times F_{original}$
로켓 엔진의 일률은 일정하므로 $v_e$는 다음과 같아야 함
$v_e = \frac{v_{e,original}}{n}$
따라서 질량 흐름 $\dot{m}_e$는
$\dot{m}_e=n^2 \times \dot{m}_{e,original}$
배기 속력이 1/n으로 감소하고, 추진체 흐름은 n^2배 증가했음.
만약 원자로를 펄스화한다면 순간 일률이 n배 증가한다고 하면(원자로에 대해서는 밑에 설명하겠음) 추진체를 n배 증가시키는 것만으로도 추력을 n배 증가시킬 수 있음.
물론 단순히 추진체 양을 단순히 늘린다고 늘린 만큼 선형적으로 추력이 증가하지는 않고 Dittus-Boelter correlation에 따라 다음과 같이 변함.
$h = h_o(\frac{\dot{m}_c}{\dot{m}_{c,original}})^{0.8}$
ISP 증가
로켓의 배기 속력은 다음과 같이 나타낼 수 있음:
$v_e \sim k\prime\sqrt{\frac{T_p}{M}}$
자세한 식은 다음과 같음(https://en.wikipedia.org/wiki/Rocket_engine_nozzle)
여기서 $T_p$는 추진체의 온도 M은 배기 가스의 몰 질량이고 k는 상수임.
따라서 ISP를 증가시키기 위해서는 추진체의 온도를 증가해야 함.
하지만 추진체의 온도 = 원자로의 온도를 증가시키는 데에는 한계가 있음. 원자로 구성 물질이 녹아버린다는 것임.
원자로를 펄스로 작동시킨다면 일반적으로 작동시킬때보다 훨씬 많은 고에너지 중성자(Fast neutron)가 순간 동안 방출됨. 따라서 순간적으로 추진체를 높은 온도로 데울 수 있음.
중성자의 운동에너지로 연료를 가열하므로 추진체의 온도가 원자로보다 높아도 열역학 법칙을 위반하지 않음.
따라서 ISP의 증가는 다음과 같음:
$I_{sp} = I_{sp,oirginal} \sqrt{f_t f_n N + 1}$
$f_t$는 일정 시간(1초) 동안 만든 펄스의 수, $f_n$은 즉각적으로 나오는 에너지의 비율, N은 기존 모드 대비 펄스 모드의 에너지 비율
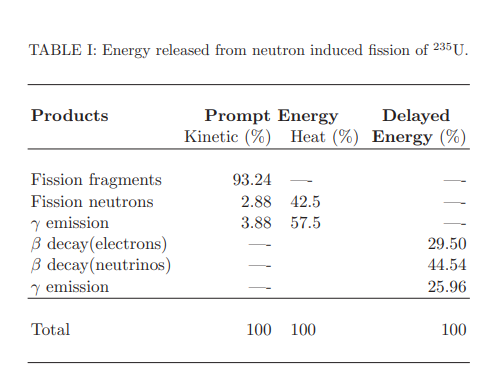
$f_n$은 표에서 보다시피 대략 6% 정도이고(감마선 포함) N은 100 정도 된다고 가정하면 초당 1펄스라고 해도 2~3배 이상의 $I_{sp}$ 증가가 가능함.
문제는 위에서 보다시피 이 원자로는 $f_n N$만큼의 에너지만을 사용하는데 그 양이 대략 6%정도라는것임.
나머지 원하지 않는 에너지들(핵분열 부산물들의 붕괴열)을 제거해주어야 하고 이 에너지들을 빠르게 제거할 수 있어야 엔진을 연속적으로 작동시킬 수 있음.

펄스 모드 대 일반 모드의 에너지 비율
펄스 모드 대 일반 모드의 에너지 비율은 다음 식으로 구할 수 있음:
$N = \frac{c_f p_f R_f^2}{4 \pi k_f(T_f-T_s)}[\frac{\triangle T}{t}]$
식의 유도 과정:
$E_{pulse} = c_f M_f \triangle T$
$E_{pulse}$ 는 펄스 과정에서 원자로에 저장된 열 $c_f$ 는 핵연료의 열용량 $M_f$는 연료의 질량 $\triangle T$는 펄스 당 온도 변화
$E_{stationary} = \chi_l lt$
$E_{stationary}$는 일반 모드에서 작동할 때의 열 $\chi_l$은 길이 당 연료의 일률, l은 핵연료의 길이, t는 연료가 연소실에 머무는 시간
여기서 핵연료가 원통형이므로 $M_f = \pi R_f^2 l \rho_f$, $\chi_l = 4\pi k_f(T_f-T_s)$
$R_f$는 연료의 반지름, $\rho_f$는 연료 밀도, $k_f$는 열전도율, $T_f$는 핵연료 중앙 온도, $T_s$는 핵연료 표면 온도
따라서 E_pulse를 E_stationary로 나누면 N을 구할 수 있음.
물론 이건 아주 단순화한 식이고 원래 논문에서는 베셀 방정식 사용해서 푸는 게 있는데 그 식은 여기서 다루지는 않겠음. 목표가 적절한 N 값을 구하는 것이므로 위의 간단한 식으로도 충분히 가까운 값을 구할 수 있음.
현실에 존재하는 원자로의 값을 대입해보면:
$c_f \approx 300J / (mol \cdot K)$, $k_f \approx 6W/(k \cdot m^2)$, $\rho_f=10^4kg/m^3$, $R_f ~ 10^{-2}m$, $T_f - T_s = 600K$ 정도이므로
$N \approx 6 * 10^-3[\frac{\triangle T}{t}]$
$\frac{\triangle T}{t}$는 t가 10^{-3}초 정도이고 $\triangle T$가 10^3K 이상이므로 대략 10^6 이상 되는 값임.
이 정도의 온도 변화는 비정질 금속 제련 과정에서 볼 수 있음.
따라서 N은 100~1000사이의 값을 가짐.
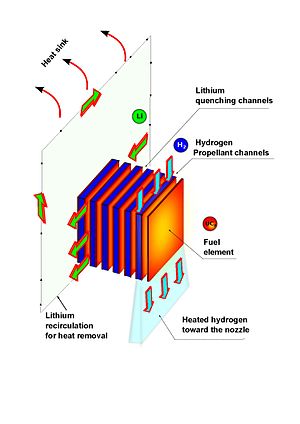
원자로
원자로에는 핵분열 후 바로(10^-14초 이내) 튀어나오는 prompt neutron과 핵분열 생성물에서 베타 붕괴와 같이 튀어나오는 delayed neutron이 있음.
여기서 원자로와 핵폭탄의 차이를 알 수 있음.
생성된 중성자 양/중성자가 흡수되는 양을 Effective neutron multiplication factor(k)라고 하는데
k < 1이면 핵분열 연쇄 반응은 언젠가 멈춤(subcritical)
k = 1이면 일정한 출력을 얻을 수 있음(critical)
k > 1이면 핵분열 반응이 지수함수적으로 증가함(supercritical)
원자로는 k값을 1 언저리로 유지하지만 핵폭탄은 k값이 1 이상임.
원자로는 최대 몇 분에 걸쳐 나오는 delayed neutron이 작은 비율로 있기(0.7%) 때문에 원자로의 출력을 꺼지지 않을 정도로 조절할 수 있지만, 핵폭탄은 수 나노초 안에 나오는 prompt neutron만을 사용할 수 있기 때문에 핵반응을 제어할 충분한 시간이 없음.
여기서부터 높은 펄스 출력을 낼 수 있는 원자로에 대해 설명해보겠음.
TRIGA 원자로는 펄스 과정에서는 원자로에서 제어봉을 빼서 연쇄 반응을 순간적으로 supercritical 상태로 만듬. 그러면 원자로의 온도는 급격히 상승하고 핵연료가 흡수하는 중성자 양은 감소함. 따라서 핵분열 반응이 감소하고 다시 정상 상태로 되돌아옴.
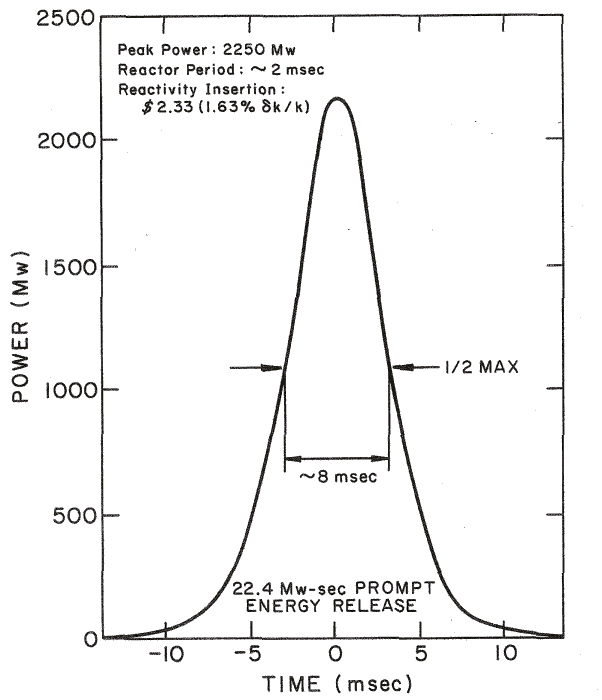
일반적인 원자로는 즉각적인 핵분열 반응에서 나오는 열 에너지가 위의 표에서 보다시피 6% 정도밖에 안되고 나머지는 핵분열 부산물에서 나오지만, 이 원자로는 6%의 에너지를 매우 짧은 시간 동안 매우 높은 출력으로 사용할 수 있음.
TRIGA 원자로는 전력 출력이 16MW밖에 안되지만 펄스 모드로 작동한다면 최대 22000MW의 전력을 만들 수 있음.
이 원자로를 쓰는 목적은 액체수소를 가열할 정도로 많은 양의 fast neutron을 얻어내는 것이고, 그걸 원자로 멜트다운이나 체르노빌화 없이 얻어낼 수 있으므로 pulsed NTR을 현재 기술로 만들 수 있다는 것을 알 수 있음.
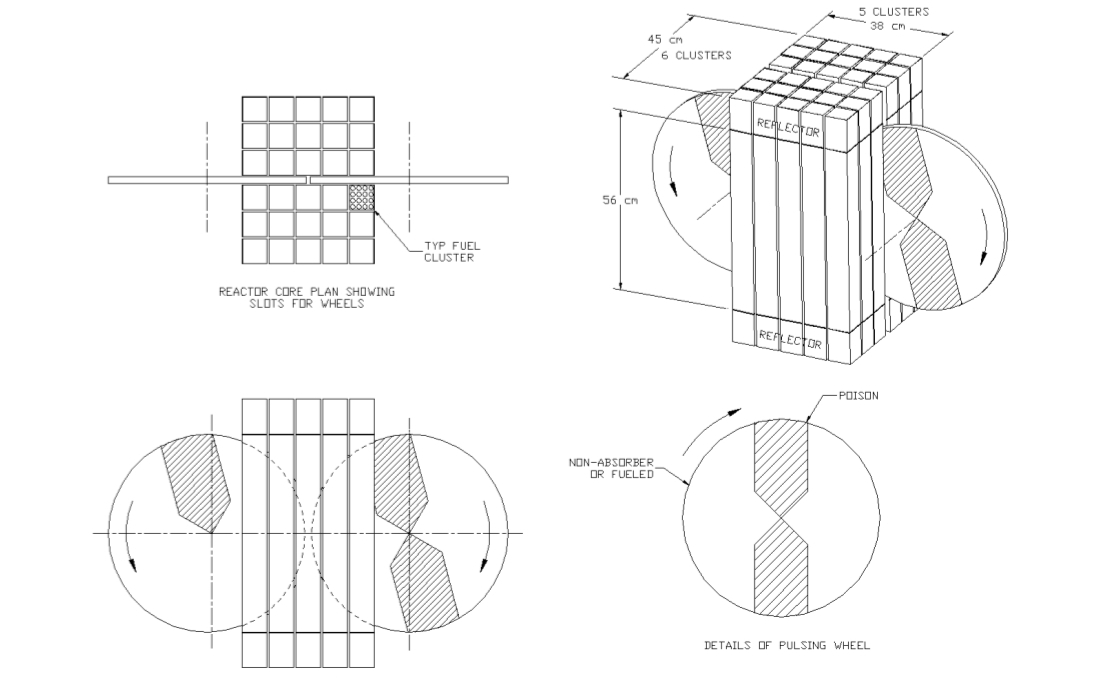
이렇게 온도를 이용하지 않고 중성자 독과 핵분열 물질을 원반으로 만들어서 펄스 원자로를 만들 수도 있음.
펄스 원자로 냉각
위에서 설명했다시피 원자로에서 나오는 94%의 에너지는 그대로 열로 배출되므로 냉각이 필요함.
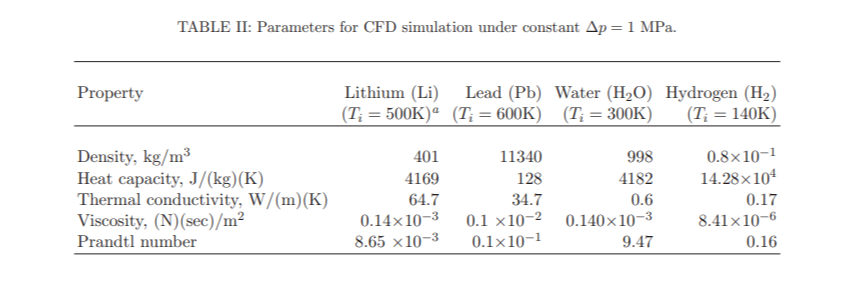
이 논문에서는 리튬이 증기압이 낮고 밀도도 낮고 열용량은 높으며 점성이 작고 순환하는 데 에너지가 적게 든다고 리튬을 냉각재로 쓰자고 주장함.
논문에 따르면 초당 제거해야 하는 열은 원자로 지름이 1m일때 16.8MW인데 SSME의 터보펌프가 수소를 1.9MPa에서 45MPa까지 압축할 수 있으니까 가능한 범위라고 함. (1Pa = 1kg/m s^2, 1W = kg m^2 / s^3)
물론 냉각재만 있다고 되는게 아니기 때문에 복사 냉각 방식으로 리튬의 열을 우주로 배출해야 하지만, 많은 양의 열을 상대적으로 작은 크기와 무게의 라디에이터로 빼내는 기술은 이미 있음.
정리
이미 테스트 된 기술인 열핵 로켓의 비추력을 최소 5배 이상(N > 600) 올릴 수 있는 기술은 지금의 기술로도 충분히 실현 가능하고, 추력의 손실 없이 달성 가능함. 위의 회전 원반만으로도 10kHz 정도의 펄스를 달성할 수 있고 레이저를 사용한다면 그 이상도 가능함.
참고자료:
https://en.wikipedia.org/wiki/Pulsed_nuclear_thermal_rocket#cite_note-arias16-1
Pulsed nuclear thermal rocket - Wikipedia
A sequence for a stationary-pulsed-stationary maneuver for a pulsed thermal nuclear rocket. During the stationary mode (working at constant nominal power), the fuel temperature is always constant (solid black line), and the propellant is coming cold (blue
en.wikipedia.org
https://arc.aiaa.org/doi/10.2514/6.2016-4685
On the Use of a Pulsed Nuclear Thermal Rocket for Interplanetary Travel | AIAA Propulsion and Energy Forum
Copyright © 2016 by Francisco Javier Arias Montenegro. Published by the American Institute of Aeronautics and Astronautics, Inc., with permission.
arc.aiaa.org
'Space > 로켓' 카테고리의 다른 글
| VASIMR, 자기 노즐, 핵융합로 (0) | 2023.01.19 |
|---|---|
| Magnetoplasamadynamic thruster (0) | 2021.12.05 |
| Hall effect thruster (3) | 2021.10.24 |
| Gridded ion thruster (0) | 2021.10.18 |
| Beal Aerospace BA-2 (0) | 2021.02.20 |




댓글