1차원 슈뢰딩거 방정식 시뮬레이션

일단 만들었음.

https://github.com/hydrogendeuteride/Schrodinger_1D/tree/master

GitHub - hydrogendeuteride/Schrodinger_1D: C++ schrodinger equation solver with opengl graph

슈뢰딩거 방정식을 컴퓨터로 푸는 건 꽤 간단함.

 

$H\psi = E\psi$에서 $\psi$는 슈뢰딩거 방정식의 고유 벡터이고 $\psi$를 유한한 벡터라고 하면 H는 정사각 행렬이고 E는 고유값임.

 

따라서 슈뢰딩거 방정식의 고유 상태는 행렬의 고유값 문제를 풀기만 하면 됨.

 

선형대수 라이브러리를 처음부터 만드는 건 이런 데 파이썬을 쓰지도 않고 OpenGL을 쓸 정도로 정도로 시간낭비를 좋아하는 나에게도 너무 쓸데없는 짓이라 여겨지기 때문에 Eigen 라이브러리를 사용했음.

void FDM_Solver::Solve(const std::vector<double> &Potentials)
{
    for (int i = 0; i < num_grid - 2; ++i)
    {
        Hamiltonian(i, i) = 1.0 / (dx * dx) + Potentials[i + 1];

        if (i != num_grid - 3)
        {
            Hamiltonian(i, i + 1) = -1.0 / (2.0 * dx * dx);
            Hamiltonian(i + 1, i) = -1.0 / (2.0 * dx * dx);
        }
    }

    Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> s(Hamiltonian);

    Eigen::MatrixXd eigenvectors = s.eigenvectors();
    const Eigen::VectorXd& eigenvalues = s.eigenvalues();

    EigenVector = Eigen::MatrixXd(num_grid, eigenvectors.cols());

    for (int col = 0; col < eigenvectors.cols(); ++col)
    {
        EigenVector(0, col) = 0.0;
        for (int i = 1; i < num_grid - 1; ++i)
        {
            EigenVector(i, col) = eigenvectors(i-1, col);
        }
        EigenVector(num_grid - 1, col) = 0.0;
    }

    EigenValue = eigenvalues;
}

파이썬이였으면 한줄로 풀었음.

 

해밀토니안 행렬을 구축하고 고유값과 고유벡터를 구해서 클래스의 변수에 저장하는 함수임.

 

웨이브 패킷을 시뮬레이션하는 것 역시 컴퓨팅 자원이 아깝지 않다면 쉬움.

 

공간을 아무튼 유한하게 나누기 때문에 FDM 방법임.

void Wave_Packet::TimePropagate(double dt, const Eigen::MatrixXd &Hamiltonian)
{
    Eigen::MatrixXcd H_complex = -std::complex<double>(0, 1) * Hamiltonian * dt;
    Eigen::MatrixXcd U = H_complex.exp();

    Packet = (U *  Packet).real();

    normalize();
}

웨이브 패킷에 시간 의존성 $e^{-iHdt/\hbar}$을 곱해주면 됨.

하지만 이렇게 하면 겨우 격자 256개짜리 시뮬레이션도 실시간으로 돌릴 수 없고 나는 실시간으로, 안정적으로 시뮬레이션을 돌리고 싶음.

 

이 방법은 행렬 * 벡터 연산이므로 시간 복잡도가 $O(n^2)$임.

void Wave_Packet::TimePropagate(double dt, const std::vector<double> &Potential)
{
    std::vector<std::complex<double>> WaveFunction;
    for (int i = 0; i < Packet.size(); ++i)
    {
        WaveFunction.emplace_back(Packet[i].real(), Packet[i].imag());
    }

    for (int i = 0; i < WaveFunction.size(); ++i)
    {
        WaveFunction[i] *= std::exp(-I * Potential[i] * dt / 2.0);
    }

    FFT::FFT(WaveFunction);

    double dk = 2 * PI / Grid_Num;
    for (int i = 0; i < Grid_Num; ++i)
    {
        double k = i < Grid_Num / 2 ? i * dk : (i - Grid_Num) * dk;
        double energy = 0.5 * k * k;
        std::complex<double> phase(0, -energy * dt);
        WaveFunction[i] *= std::exp(phase);
    }

    FFT::IFFT(WaveFunction);

    for (int i = 0; i < WaveFunction.size(); ++i)
    {
        WaveFunction[i] *= std::exp(-I * Potential[i] * dt / 2.0);
    }

    for (int i = 0; i < WaveFunction.size(); ++i)
    {
        Packet[i] = WaveFunction[i];
    }

    normalize();
}

그래서 더 빠르게 풀기 위해 사용한 split operator method.

https://www.sciencedirect.com/science/article/abs/pii/S0096300304008689

Numerical studies on the split-step finite difference method for nonlinear Schrödinger equations

얘로는 이제 비선형 슈뢰딩거 방정식을 풀 수 있음.

 

$e^{-i\hat{H}\Delta t/\hbar}\approx e^{-i\hat{T}\Delta t/2\hbar}e^{-i\hat{V}\Delta t/\hbar}e^{-i\hat{T}\Delta t/2\hbar}$

이렇게 시간 간격을 1/2씩 진행하기 때문에 룽게-쿠타 방법처럼 그냥 좌변처럼 해밀토니안 행렬을 곱해서 구할 때보다 더 정확함.

 

하지만 나는 여기에 spectral method를 적용하기로 했음. 이유는 딱히 없고 그냥 고속 푸리에 변환 복습하고 싶어서임.

스펙트럴 방법은 슈뢰딩거 방정식의 해처럼 부드러운 해에 대해 높은 정확도를 가진다고 함.

$\psi (x, t+ dt) = e^{--i\hat{V}\Delta t/ 2 \hbar} \mathcal{F}^{-1}(e^{-i\hat{T}\Delta t/\hbar}\mathcal{F}(e^{-i\hat{V}\Delta t/2\hbar} \times  \psi (x, t)))$

 

이렇게 운동 에너지 계산항 전후로 푸리에 변환, 역변환을 만들어줌.

 

패킷을 위치 공간에서 1/2이동하고, 운동량 공간에서 1만큼 이동 후 다시 위치 공간에서 1/2 이동함.

고속 푸리에 변환이 사용되었으므로 시간 복잡도는 $O(n \log n)$임.

 

이제 스펙트럴 방법에 대해 설명하겠음.

푸리에 변환된 함수의 미분은 다음과 같음.

$\frac{d f}{d x}=\sum_{n=-\infty}^{\infty}i k_{n}{\hat{f}}_{n}e^{i k_{n}x}$

따라서 주파수 공간에서의 미분은 벡터의 곱셈으로 볼 수 있음

 

따라서 라플라시안 연산자는 다음과 같음:

$\nabla^{2}\to-k^{2}$

 

슈뢰딩거 방정식은

$i\hbar{\frac{\partial}{\partial t}}\psi=-{\frac{\hbar^{2}}{2m}}\nabla^{2}\psi+m V\psi$

이렇게 생겼는데

 

퍼텐셜 에너지 항을 제외하고 보면:

$i\hbar{\frac{\partial}{\partial t}}{\hat{\psi}}={\frac{1}{2}}k^{2}{\hat{\psi}}$

 

이 계산은 위의 코드에서 FFT 함수들 사이에 있는 부분에 해당함.

 

---

글 쓴날(23.9.2) 현재 진행상환

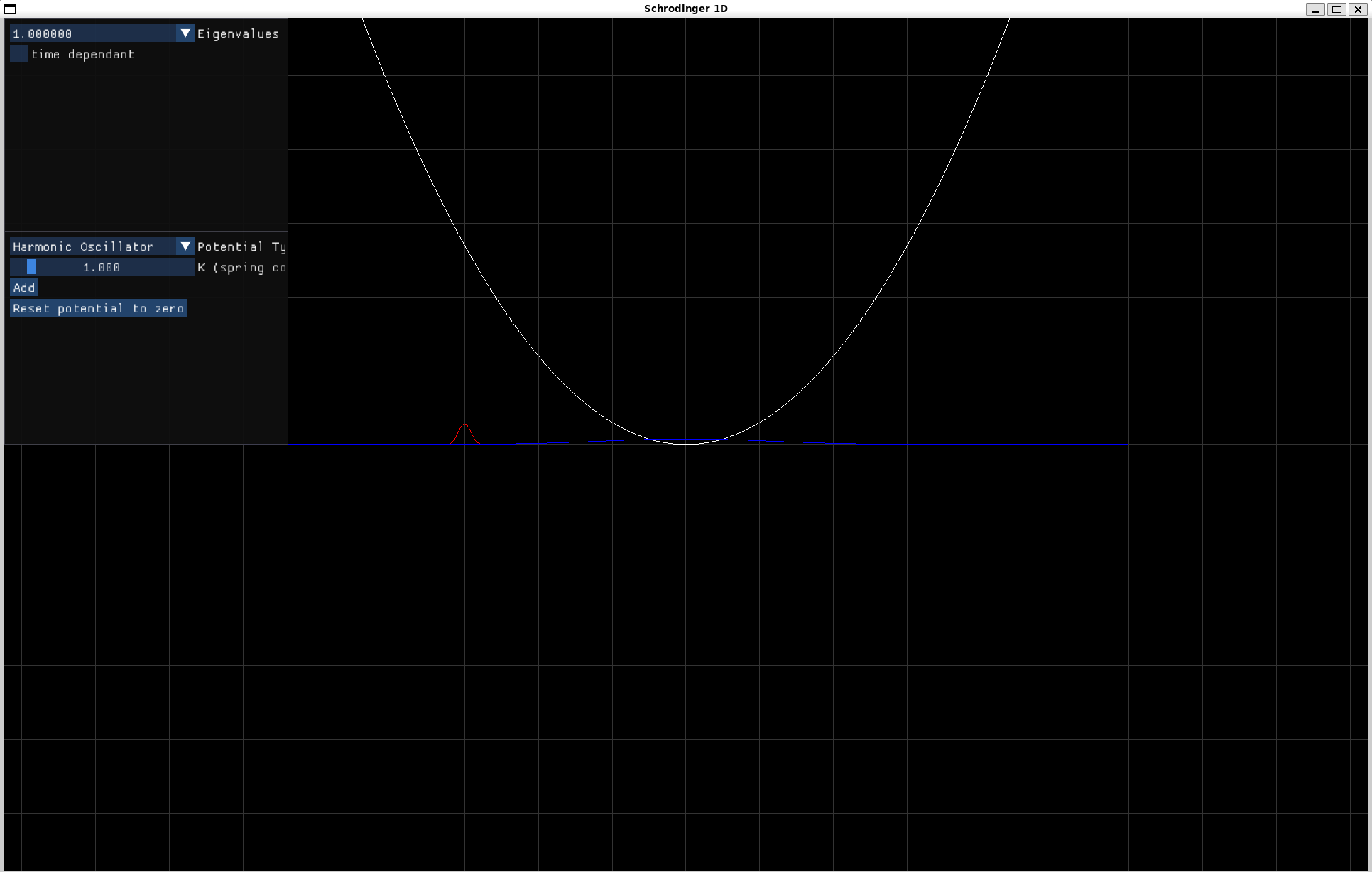
이 외에도 cubic spline, FFT 등을 c++ 표준을 이용해서 바닥부터 만들어보았지만, 글에 어울리는 주제는 아니니까 넘어가고 2차원이나 3차원으로 만드는 것도 어렵지는 않지만, 격자가 많아지면 계산 시간이 매우 많이 늘어나서 GPGPU 같은 걸 사용해야 하지만, 방학 때 공부하다 우선순위가 밀린 관계로 만들지는 않았음.

 

파동 방정식 프로그램도 아직 블로그에 제대로 쓰지도 않아서 그것도 써야 하고, 이 프로그램도 여러 가지 조건을 추가하고, 계산 속도를 향상시키는 등의 개선을 해야 하는데 개학해버려서할 수 있을지는 모르겠음.

 

아마 다음 프로젝트는 Barnes-Hut 태양계 시뮬레이터 with OpenGL(람베르트 솔버, Reference Frame 변환, 저추력 궤도 등등)일 것 같음.

 

 

참고:

 

Accelerating the Fourier split operator method via graphics processing units