*마크론(Macron)은 물리에서 먼지 크기의 작은 입자를 말하고 이 글에서 먼지 또는 입자 정도로 대체해서 사용하겠음
*구글에 macron으로 검색하면 프랑스 대통령밖에 안나와서 검증에 고생 좀 했음
*https://iopscience.iop.org/article/10.1088/0032-1028/9/2/308
*https://ntrs.nasa.gov/citations/20180004500

다양한 방법으로 마이크로미터 크기의 먼지를 10~10000km/s 로 가속하는 방법에 대해 알아보고 우주에서의 사용에 대해 알아보겠음.
빠르게 가기 위해 작게 만들기

미세 입자는 현미경으로 볼 수 있는 복잡한 구조와 원자를 셀 수 있을 정도의 분자 중간에 위치하는 먼지임.

전형적인 미세 입자는 지름이 마이크로미터 수준이고 구조가 단순함. 작은 크기 때문에 표면적 대 질량 비가 매우 높음. 따라서 질량에 비해 많은 전하를 띨 수 있고, 정전 가속기에서 유용하게 사용할 수 있음.
작은 입자는 레일건의 가열과 마찰에서 살아남기 힘듬. 그리고 코일건의 강력한 자기장에서도 버티지 못함. 그러나 정전 가속기는 전압 구배를 이용해서 입자를 빠르게 가속할 수 있음. 미세 입자는 표면적이 넓어서 강한 전하를 띠므로 전압 구배 속에서 높은 가속력을 받을 수 있음.
입자의 속도(m/s) = (2 * 전압(V) * 단위질량 당 전하(C/kg)) ^ 0.5
정전 가속기는 작은 물체를 빠른 속도로 발사할 때 사용됨. 예를 들어서 콜로이드 추력기 같은 전기추진 로켓은 작은 물방울을 초속 수 킬로미터로 발사함. 이것이 우리가 원하는 미세 입자 가속기와 비슷함. 어떤 콜로이드 추력기는 물방울을 43km/s로 가속함. 정전 가속기는 의료 현장에서도 볼 수 있는데, 주로 X선을 발생할 때 사용함.

가장 강력한 정전 가속기는 핵 연구 목적으로 만들어졌고, 수 MV로 작동하며 전자와 이온을 가속함.

반데그라프 가속기는 행성간 미세먼지를 테스트하기 위해 사용됨. 가속기는 1962년에 Friichtenicht에 의해 지어졌고 0.1마이크로미터 철 구를 2MV 구배로 14km/s로 가속할 수 있었음. 또, 정전 가속기에는 Cockroft-Walton이나 Marx, Pelletron등이 있고, 각각의 방식으로 높은 전압을 만들어냄.
그러면 얼마나 높은 전압을 얻을 수 있을까?

1V 차이가 1m 사이에 있다면, 구배는 1V/m임. 1000V가 1cm 사이에 있다면, 100000V/M임. 구배는 입자를 가속할 수 있는 힘을 주지만, 전자도 그 사이를 뛰어넘어서 반대쪽 전극으로 가서 전극을 손상시키고 전압 구배를 낮춤.

약한 전압 구배이더라도 소금물같은 도체가 사이에 있다면 전자가 쉽게 뛰어넘음. 강한 구배를 위해서는 순수한 진공같은 부도체가 필요함. 만약 전극 표면이 고르지 않다면, 전하는 한 곳으로 집중될 것이고, 전체적인 전압 구배는 낮아질 것임. 전압 구배가 너무 높다면 전자가 건너뛰면서 아크 방전이 일어남. 아크 방전으로 손실된 에너지는 하전 입자로 전달되지 않고, 전극을 태우기만 함. 메가와트~기가와트 급의 장치에서 아크 방전이 발생하는 것을 누구도 바라지 않을 것임.
1단 정전 가속기는 10~15 MV 정도의 전압을 갖고, 이보다 더 높은 값을 갖는 건 voltage multiplier circuit 부분이 점점 커지면서 많은 문제가 생김.

위의 사진은 30MV Pelletron임. 높은 전압은 전극 사이가 절연 기체로 채워져있기 때문에 가능함. 그러나 하전 입자와 기체가 일으키는 마찰열 등을 생각해보면 우리는 이 기체를 사용할 수 없음. 우리는 진공에 의존해야 함. 또, 미세 입자는 빠르게 전하가 바뀔 수 없음.

Supre Marx Generator는 1000MV 이상의 전압을 얻기 위해 사용됨. 길이가 1500m 이므로 구배는 0.6MV/m임. 이 디자인은 수 기가줄의 에너지를 저장함. 우리의 미세 입자들은 그 정도로 많은 에너지가 필요하지는 않지만, 요구되는 길이 조건은 충족함. 100MV를 내기 위해서는 167m이 필요할 것임.

다른 대안은 다단 가속기임. 정전 가속기를 여러 개로 나눠서 각각의 전압 구배로 입자를 가속함. 만약 가속되는 환경이 완전히 진공이고 오염 없이 평평한 전극이라면 1~10MV/m을 달성 가능함. Super Marx Generator보다 뛰어나지만, 현실적으로는 3MV/m이 가능함.

미세 입자가 판을 가로지르는 짧은 시간동안만 작동된다면 여러 단계의 전기 펄스로 가속할 수 있음. 이 디자인은 5단으로 설계되서 실험된 적이 있음. 100MV로 가속할 때 10~100m 정도만 필요함.
단점은 전극을 바꾸는 게 쉽지 않다는 것임. 트랜지스터 같은 스위치들은 전기 에너지를 열 에너지로 전환하면서 많은 에너지를 소비함.
원형 가속기를 생각해볼 수도 있음.

수천 개의 가속 단 대신 한 개의 가속기를 계속 사용할 수 있음. U자형 자석에서 미세 입자는 180도 꺽이면서 원 궤적을 만듬. 따라서 가속기의 전압 구배가 클 필요가 줄어듬. 그러나 자석이 미세 입자의 궤적을 충분히 휠 수 없는 속도에서는 사용이 불가능함.
최대 속도(m/s) = 휘어지는 반지름(m) * 자석 세기(T) * 전하 대 질량비(C/kg)
이 가속기에서는 전압 구배는 성능에 영향을 끼치지 않음. 단지 회전을 더 하면 할수록 속도가 빨라질 뿐임.

반지름이 클수록 자석의 세기를 낮출 수 있음. 그러나, 우주선의 단면적이 무한히 커질 수는 없기 때문에 커다란 원형 가속기는 무리가 있고, 선형 가속기가 더 자주 쓰일 것임. 그러나, 선형 가속기의 최대 속도는 전하 대 질량비의 제곱근에 비례하지만, 원형 가속기에서는 비례하므로, 전하 대 질량비가 증가할수록 원형 가속기가 더 이득임.
우주선에서 두 가지 종류의 가속기를 결합해서 사용한다면 최대 속도를 늘릴 수 있음.
가속기에서 빠져나온 뒤에 미세 입자는 얇은 플라즈마나 입자빔 등으로 중성화될 수 있고, 목적지에 도달할 때 까지 탐지하기 매우 어려움.
전하 대 질량 비
가속기의 질량을 줄이기 위해서는 더 낮은 전압과 더 높은 질량 대 전하비가 필요함.
구형 미세입자의 경우 반지름이 작아질수록 표면적 대 부피 비가 감소함. 10배 작은 반지름을 가지는 구는 표면적 대 부피 비가 10배 뛰어남. 이 말은 10배 뛰어난 질량 대 전하비를 얻을 수 있다는 것임.
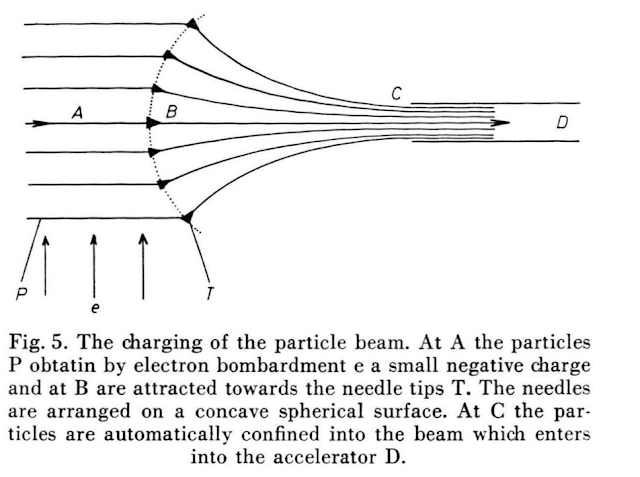
전하는 다양한 방법으로 얻을 수 있음. 구체는 얼마나 많은 전하를 저장할 수 있을까?
전체 전하 = 표면에 있는 전하이므로(표면에 전하가 있을 때 가장 많은 전하를 저장할 수 있음, 표면전하 참조)
표면 전하(C) = 1.11 *10 ^ -10(4*pi* 진공 유전율) * 전압 구배(V/m) * 반지름(m) * 2
이고,
질량 당 전하 = 2.655 * 10^-11 * 전압 구배 / (반지름 * 밀도) 임
이 공식들에 따르면 전하 대 질량비를 최대화하기 위해서는 반지름은 최대한 작아야 하고, 전압 구배는 최대한 커야 함. 음전하를 띠는 미세 입자는 전압 구배가 100MV/m 정도임. 만약 양전하라면, 1000MV/m 까지 가능함. 다른 소스에서는 50000MV/m까지 가능하다고 하지만, 이는 이론적 한계값에 가까움. 만약, 입자가 너무 많이 대전되어 있다면, 전계 방출이 일어나고, 작은 먼지는 스스로를 파괴할 것임.
우리가 가속하고자 하는 먼지들은 이 정도 한계까지 도달할 것임.

1mm 지름의 양전하로 대전된 철로 된 구체가 있다고 하면, 지름은 5 * 10^-4m 이고 밀도는 8600 kg/m^3임. 질량 당 전하 비는 0.006C/kg임.
1 마이크로미터 질량의 리튬 구가 있다고 생각한다면, 반지름은 0.5마이크로미터이고 밀도는 534kg/m^3임. 질량 대 전하 비는 99C/kg임.
위의 예시에서 리튬 구는 철제 구보다 지름이 작고 밀도가 낮아서 훨씬 유리함을 알 수 있음.

다른 한계는 먼지의 강도임. 물질이 전압 구배를 견디는 힘은 물질의 인장 강도와 관계가 있음. 먼지가 견딜 수 있으 최대 질량 대 전하 비는 다음과 같음.
인장 강도에 제한된 질량 대 전하 비(C/kg) = (1.77 * 10^-11 * 인장 강도(Pa)) ^0.5 / (반지름(m) * 밀도)
전에 예시로 들었던 철제 구는 인장 강도가 250MPa이므로 0.015C/kg를 버틸 수 있음. 이전에 계산했던 값의 절반 정도임.
리튬은 인장 강도가 15MPa 정도라서 의의 예시에 나온 리튬 구는 0.99C/kg 밖에 버티지 못함.
더 많은 질량 대 전하 비를 얻기 위해서는 더 강한 물질이 필요함. 그러나 작은 먼지들은 또 다른 장점이 있음. 매우 작은 크기에서는 물질은 결점 없이 생산될 수 있음. 이 때문에 물질을 최대한 활용할 수 있게 됨.
좋은 예시는 철임.

일반적인 철 인장 강도가 250MPa 수준임. 그러나 마이크로미터 길이의 철 monocrystalline whisker는 인장 강도가 14000 MPa임. 그래서 0.12C/kg까지 수용할 수 있음.
일반적인 물질들과 마이크로미터 크기의 물질들 사이의 강도 차이는 여기서 찾아볼 수 있음.
질화규소 whisker는 인장 강도가 13800 MPa이고, 3200 kg/m^3이므로 kg 달 309C를 저장할 수 있음.
최강의 재료는 탄소섬유임. T1100g 탄소 섬유는 질량이 가벼우면서 강도가 강한 물질 중에서 가장 상업화된 물질임. 7000 MPa를 견딜 수 있고, 밀도는 1790 kg/m^3임. 마이크로미터 크기의 구형 탄소 섬유는 393C/kg를 저장할 수 있음.

마이크로미터 크기에서는 탄소 섬유도 탄소 나노 튜브의 엄청난 특성을 얻음. T1100G의 10배에 달하는 인장 강도(63000 MPa) 로 1576C/kg를 저장할 수 있음.
만약 질량 대 전하 비에서 전계 방출의 한계에 부딫힌다면, 이런 작은 물질들의 잠재력을 어떻게 끌어낼 수 있을까?
먼지의 모양 바꾸기
질량 대 전하 비를 늘리는 방법은 단순한 구체에서 벗어나는 것임.

이 구들은 내부가 빈 상태로 만들 수 있음. 내부를 비우면 질량 대 전하 비가 증가함. W를 반지름 대 껍질 비율로 정한대면 W = 0.5는 반지름 의 절반이 껍질이란 것이고, W = 0.01은 껍질의 두께가 반지름의 백분의 일 정도라는 것임.
껍질의 두께는 이전에 구했던 식의 밀도에 곱해서 빈 껍질의 전계 방출에 제한된 전하를 알 수 있음
질량 당 전하 = 2.655 * 10^-11 * 전압 구배 / (반지름 * 밀도 * W) 임
질량 당 전하는 껍질의 두께에 반비례해서 증가함.
그러나, 빈 껍질은 얇은 만큼 더 낮은 강도를 가지고 있기 때문에 인장력에 제한된 질량 대 전하 비도 알아봐야 함.
인장 강도에 제한된 질량 대 전하 비(C/kg) = (1.77 * 10^-11 * 인장 강도(Pa) * W) ^0.5 / (반지름(m) * 밀도 * W)
여기서는 제곱근에 반비례하기 때문에 W = 0.1이어도 3.3배의 이득만 볼 수 있음.
이 식으로 알 수 있는 것은 두께가 얇아질수록 투사체의 인장 강도가 더욱 중요해진다는 것임.
먼지를 기둥 모양으로 만드는 방법도 있음.
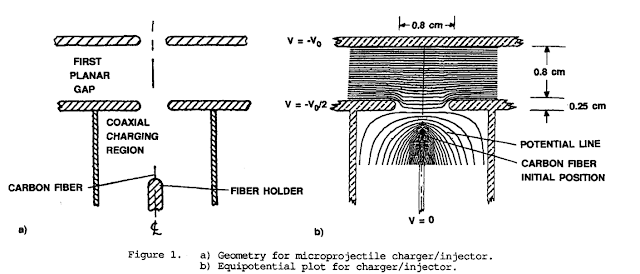
원통형으로 만들면 길게 만들어서 구형에 비해 질량 대비 표면적을 늘릴 수 있고 질량 대 전하 비를 더 늘릴 수 있음.
원통의 지름 대 길이 비를 G 라고 하고, 같은 부피의 구와 표면적을 비교하면:
원통 대 구의 표면적 비율 = 0.605 * G^0.333
만약 G가 2000 정도 된다면 같은 부피의 구보다 표면적이 7.6배 더 커짐. 탄소나노튜브처럼 몇 센치미터 길이의 입자는 G 값이 10000000에 달하고 131배나 더 커짐.
원통도 구처럼 속이 빈 모양을 취할 수 있으므로 위에 세운 공식과 비슷한 결과를 기대해볼 수도 있음.
이온 빔으로 먼지 가속하기
정전 가속기는 먼지를 완전히 다른 방법으로도 가속할 수 있음.
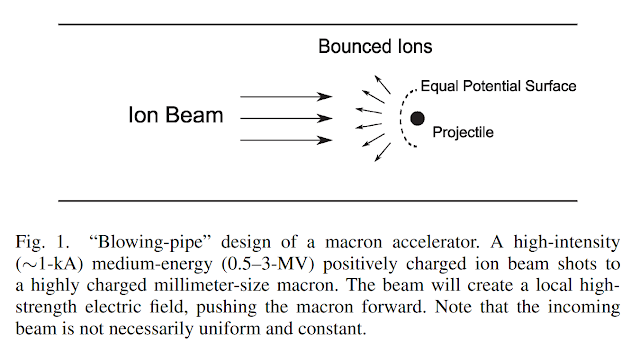
직접 전기장을 이용해서 미세 입자를 밀어내는 대신 전자/양성자를 이용해서 가속할 수도 있음. 이 방법을 beam pushrod 방식 또는 빔 공기총(blowpipe) 방식이라고도 함.
대전된 먼지는 같은 전하로 대전된 물체를 밀어냄. 이 먼지의 내부 전압 구배는 1000MV/m이고 길이는 1mm임. 이 먼지는 500KeV 아래의 입자를 밀어낼 수 있음. 그러나 천 배 작은 먼지는 500eV 정도의 에너지를 가진 입자만을 밀어낼 수 있지만 제곱-세제곱 법칙 때문에 갈수록 가속이 더 강해짐. 음으로 대전된 먼지는 100MV/m 이상의 전압 구배를 가질 수 없고 50keV 빔을 1mm에서 밀어내거나 1um에서 50eV 빔을 밀어낼 수 있음.

에너지가 더 적은 빔은 입자를 더 먼 곳에서 밀어낼 수 있음. 그러면, 더 높은 유효 표면적으로 입자를 밀어낼 수 있음. 예를 들자면, 최대 50eV를 밀어낼 수 있는 먼지는 25eV를 1.4배 먼 곳에서 2배의 유효 표면적으로 밀어낼 수 있음. 이 논문에서 제안된 것처럼 가속기 전체에 먼지의 유효 표면적과 비슷한 면적으로 빔을 집중하는 전자기장 렌즈가 있다고 가정하면 이해하기 쉬울 것임.
먼지가 가속력에서 살아남을 수 있는지는 그 먼지의 인장 강도가 결정함.
최대 가속도 = (0.75 * 인장 강도(Pa)) / (입자 반지름 * 밀도)
이 값은 그 물체의 껍질 두께와 무관함.
밀리미터 크기의 알루미늄 7075-T651(570 MPa, 2800 kg/m^3)은 1.52*10^8m/s^2의 가속력을 받을 수 있고, 마이크로미터 크기의 다이아몬드 구(1600 MPa, 3510 kg/m^3)은 3.42*10^11m/s^2 까지 가속할 수 있음.
양전하로 대전된 먼지는 양성자 빔으로 가속해야 함. 500 keV에서는 양성자는 9780km/s의 속도를 갖고 500eV에서는 300km/s로 떨어짐.
음전하로 대전된 먼지는 전자 빔으로 가속해야 함. 50 keV에서는 전자는 123000km/s의 속도를 갖고 50eV에서는 4190km/s 임.
이 수치는 먼지가 빔의 최대 속력으로 점근하는 것을 의미하지는 않음. 만약 먼지가 4190 km/s(50eV 전자 속도)로 이동하고 있다면, 이 먼지는 100eV의 전자도 밀어낼 수 있음. 입자 가속기에서 나오는 먼지와 비슷한 속도의 입자 펄스들은 먼지의 속도를 단계적으로 더 높일 수 있음. 이 방법은 먼지에 입자의 운동량을 효과적으로 전달할 수 있음.
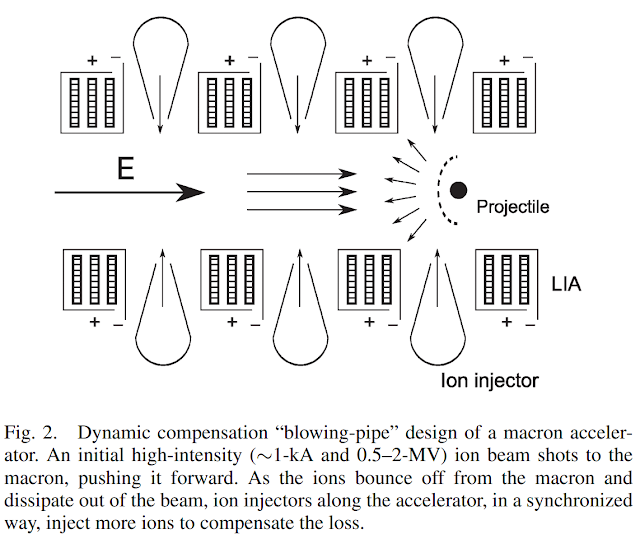
하전입자빔으로 먼지를 가속하는 건 빔의 세기에 영향을 받지 않는다는 장점이 있음. 양성자나 전자는 미세 입자를 건드리지 못하고 정전기적으로 반사되기 때문에 그 어떤 에너지도 열로 변환되지 않음. 또한, 가속관이 전자기 렌즈로 높은 빔 세기로 작동 가능함. 입자빔의 에너지는 낮지만, 그렇게 때문에 렌즈 등이 가벼워질 수 있고, 가속 튜브도 큰 질량 증가 없이 늘릴 수 있음.
pushrod 가속기의 또 다른 한계는 입자빔의 전하 밀도임.

양성자나 전자는 먼지 뒤에 고밀도로 존재하지는 않음. 같은 전하를 띠므로 서로 밀어냄. 만약 먼지 뒤에 소수의 하전 입자를 밀어넣을 수 있다면 먼지는 그 정도의 가속력만을 받게 되고 가속력은 제한됨.
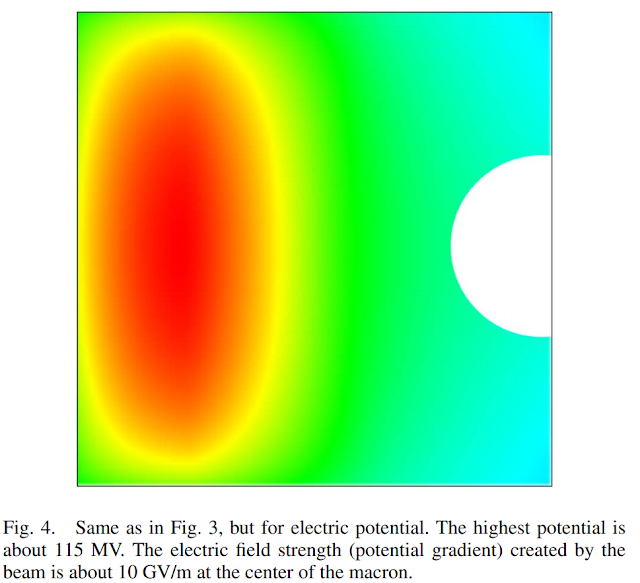
양성자나 전자가 먼지와 부딛힐 때 최대 전류 밀도는 Child-Langmuir 법칙에 의해 제한됨
최대 전류 밀도(A/m^2) = (7.7 * 10^6*빔 에너지(eV)^1.5 * 먼지 반지름) / (펄스 지속 시간 * 빔 속도)
500 keV, 1나노초 양성자 빔이 마이크로미터 크기 먼지를 밀고 있다면 빔 지름은 0.5* 10^-6m, 빔 속도는 9782000 m/s이고 최대 전류 밀도는 1.39*10^12A/m^2임.
50 eV, 1마이크로초 전자 빔이 밀리미터 크기 먼지를 밀고 있다면 빔 지름은 0.5* 10^-3m, 빔 속도는 4193200 m/s이고 최대 전류 밀도는 3.24*10^6A/m^2임.
전류 밀도와 가속력을 최대화하고 싶다면 짧은 펄스와 고에너지 양성자가 필요할 것임.
구형 먼지의 가속도는 다음과 같은 식으로 단순화할 수 있음:
펄스 가속도 = ((0.375 * 전류 밀도(A/m^2) * 빔 에너지(eV)) / (먼지 반지름 * 밀도(kg/m^3) * 펄스 지속 시간 * 먼지 껍질 두께))^0.5
500 keV, 1나노초 양성자 빔이 다이아몬드 먼지(3510 kg/m^3)를 밀고 있다면 3.85 * 10^15m/s^2 로 가속 가능함. 이 값은 다이아몬드가 버틸 수 있는 최댓값을 넘어선 값임.
50 eV, 1마이크로초 전자 빔이 알루미늄 먼지를 밀고 있다면 1.75 * 10^7m/s^2 로 가속 가능함. 이 값은 알루미늄 먼지도 충분히 견딜 수 있음.

먼지의 모양도 가속에 영향을 줄 수 있음. 평평한 판 모양은 더 넓은 빔을 잡을 수 있고, 더 많은 에너지가 먼지로 전달될 수 있음. 일렉트릭 세일 모양의 섬유 다발은 빔 접촉 면적을 최대로 늘릴 수 있음.
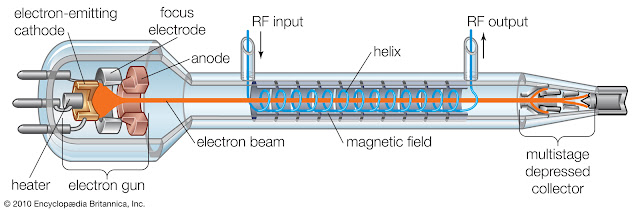
미세 입자를 미는 빔을 만드는 것은 그렇게 어렵지 않음. 저에너지 전자빔은 아주 가볍고 효율적인 장치로 만들 수 있음. 오늘날의 기술로 전자총을 만든다면 15kW/kg의 에너지 밀도로 80% 효율로 작동되게 만들 수 있음. 양성자 빔은 조금 더 까다롭지만, 그것도 작고 가벼울것임. 고주파 발생기 정도가 가장 복잡한 부분일 것임.
이 방법으로는 한 번에 하나의 입자만 pushrod 가속기에서 가속될 수 있으므로 여러 개의 가속기를 병렬로 배치하는 것도 좋은 생각임. 1나노초의 펄스를 생성하는 장치를 10개의 가속기에 동시에 공급할 수 있음. 0.1밀리초 동안 먼지를 가속한다면, 가속기 10개의 최대 발사 속도는 초당 100000개임.
가장 빠른 속도

미세 입자 가속기의 속도를 최대화하는 선택지를 아래 제시하겠음.
- 1mm 다이아몬드 구(1600 MPa, 3510 kg/m^3), 내부는 비어 있고 두께는 구 반지름의 1000분의 1임. 질량은 1.83*10^-9 kg 이고 음전하로 대전되면 1.5C/kg 까지 견딜 수 있고 양전하면 3C/kg 까지 가능함. 50 KeV 전자나 500 KeV 양성자를 반사할 수 있음. 최대 가속력 6.8^10^11 m/s^2
- 탄소섬유로 된 마이크로미터 크기 구(7000 MPa, 1790 kg/m^3), 내부는 비어 있고 두께는 지름의 100분의 1임. 질량은 9.4*10^-16이고 음전하면 296 C/kg, 양전하면 2960 C/kg 까지 버틸 수 있음. 50 eV 전자나 500 eV 양성자를 반사할 수 있음. 최대 가속력 5.8^10^12 m/s^2
- 탄소나노튜브로 된 마이크로미터 넓이, 센티미터 길이 바늘 (63000 MPa, 1000 kg/m^3), 내부는 비어 있고 두께는 지름의 10분의 1임. 질량은 7.8*10^-14이고 음전하면356 C/kg, 양전하면 3560 C/kg 까지 버틸 수 있음. 50 eV 전자나 500 eV 양성자를 반사할 수 있음. 최대 가속력 9.45^10^13 m/s^2
- Carbon nano lattice로 된 10나노미터 크기 구(200 MPa, 300 kg/m^3), 질량은 1.6*10^-22이고 음전하면 8850 C/kg, 양전하면 39665 C/kg 까지 버틸 수 있음. 0.5 eV 전자나 5 eV 양성자를 반사할 수 있음. 최대 가속력 1^10^11 m/s^2
가속기의 종류에 따라 입자의 최대 C/kg 값이 달라지고, 모든 입자는 전계 방출이나 입자 자체의 인장 강도에 따라 C/kg 값이 제한되므로 각각의 가속기 유형에 따라 가속력이 달라짐.
가속기의 종류는 다음과 같음
- 1단 10 MV 정전 가속기
- 100m 길이 다단 정전 가속기, 가속 구배 = 3 MV/m
- 100m 지름 10T 원형 가속기
- 100m 길이 전자 pushrod 가속기
- 100m 길이 양성자 pushrod 가속기
성능 수치는 다음과 같음
A1. 7.7 km/s
A2. 243 km/s
A3. 266 km/s
A4. 890 km/s
B1. 42 km/s
B2. 1332 km/s
B3. 1461 km/s
B4. 4877 km/s
C1. 1.5 km/s
C2. 1480 km/s
C3. 1780 km/s
C4. 19827 km/s
D1. 11661 km/s
D2. 721 km/s
D3. 불가능
D4. 890 km/s
E1. 11661 km/s
E2. 10392 km/s
E3. 불가능
E4. 913 km/s
큰 입자는 입자의 인장 한계에 최대 속도가 제한됨. D1과 E1에서 값이 같은 이유는 다이아몬드 구가 버틸 수 있는 최대 인장강도에 제한받기 때문임.
작은 입자의 경우 C/kg 가 충분히 크다면, 원형 가속기가 더 흥미로워짐. B와 C를 비교해보면 알 수 있음.
막대형 입자의 경우 정전 가속기에서는 정상적으로 가속이 가능하지만, blowpipe 가속기에서는 입자가 휘어버리기 때문에 가속이 불가능함.
핵분열 증폭
밀리미터 크기의 미세 입자는 몇 밀리그램을 빈 공간 속에 운반할 수 있음. 만약 그 빈 공간이 핵분열 물질로 차 있다면 충격만으로도 핵반응을 일으키기 충분함.
micro-fission에 대한 연구는 Winterberg 같은 연구자들이 이미 연구해놨음. 0.2mg 의 우라늄 235가 D-T 얼음에 덮여 있다면 10^13Pa 의 압력이 가해진다면 점화될 수 있다고 함.
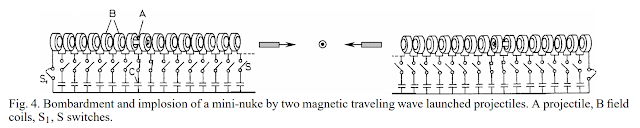
이 계산의 결과를 참조한 다른 연구에서는 D-T 얼음 안에 들어있는 우라늄의 임계 질량을 계산했는데, 20km/s 로 충돌할 경우 임계 질량은 0.04g 정도였음.
이 정도 질량의 우라늄은 지름 1.6mm 의 구 안에 들어감. DT 얼음과 10마이크로미터 두께의 탄소섬유 두께도 포함한다면 지름은 3.18mm이고 질량은 0.0422g임. 평균 밀도는 2502 kg/m^3 이고 C/kg 는 0.0067임.
3 MV/m 의 전압 구배에서는 20km/s 까지 가속하는 데 9.9km이 필요하고 10T 자석의 원형 가속기는 298.5km의 반지름이 필요함.
이 구가 버틸 수 있는 최대 가속력은 탄소섬유의 인장 강도에 제한되고, 8.29*10^6 m/s^2임. 최대 가속력으로 가속한다면 24m 길이의 가속기가 필요함. 8.44kJ의 에너지가 2.4ms 동안 소모됨.
충돌할 때 우라늄은 80TJ/kg의 에너지를 내놓고 100%의 우라늄이 연소한다면 투입한 에너지 대비 38만 배의 에너지를 얻을 수 있음.
1MW 가속기는 초당 120개의 우라늄 구를 쏠 수 있고 380GW의 에너지를 얻을 수 있음.
만약 입자의 속도가 더 빠르다면 임계 질량을 더 낮출 수 있음. 임계 질량은 속도^12/5의 비율로 줄어듬.
만약 속도가 200km/s 라면 임계질량은 0.16mg임. 이 우라늄 구는 0.252mm 안에 들어감.
DT 얼음의 두께까지 포함한다면 지름은 0.5mm 이고 질량은 0.161mg 임.

이 정도 크기의 입자는 위에 설변한 1mm 다이아몬드 구 안에 들어감. 입자의 무게는 0.00183mg 증가하고 C/kg 는 89로 조금 떨어짐. 3MV/m 의 가속기로 가속한다면 200km 정도의 길이가 필요하고 10T 원형 가속기라면 1186km의 지름이 필요함.
만약 blowpipe 가속기를 사용한다면 2.2m 의 길이만으로 200km/s 를 낼 수 있음.
더 작고 빠른 핵분열 먼지는 목적지까지 더 빠르게 도달하겠지만, 얻을 수 있는 에너지 비율은 감소할 것임.
200km/s 의 먼지는 20GJ/kg의 운동 에너지를 가지고, 핵분열로 4000배의 에너지를 방출할 수 있음. 만약 우라늄의 불완전 연소를 고려한다고 해도 여전히 전달되는 에너지는 많음.
충격 점화 핵융합
빠른 속도의 미세 입자가 충돌할 때 생기는 에너지를 이용할 수도 있음. 충돌할 때 엄청난 온도와 압력은 D-T 핵융합이 일어날 조건을 만족함.
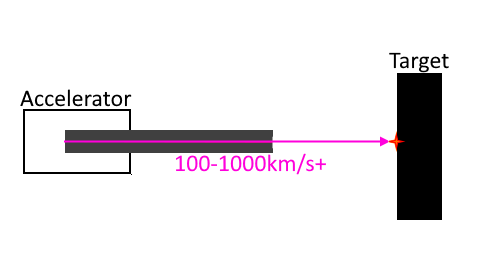
Winterberg는 충격 점화 핵융합에 대해서도 연구했음. 100km/s 의 속도는 3억 도의 온도와 핵융합 연료를 1000kg/m^3 까지 압축할 수 있다고 함.
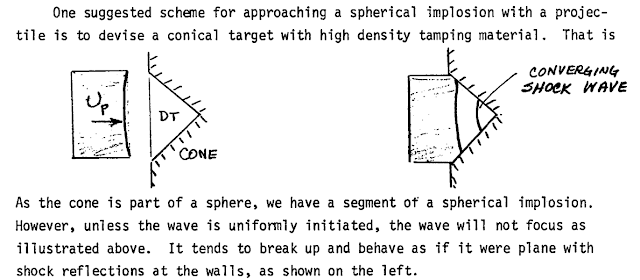
다른 소스에서는 100km/s는 잘 부서지는 껍질일 때의 경우고, 원뿔 모양으로 생긴 충돌체라면 50km/s 도 가능하다고 함.
충격 점화 핵융합은 임계 질량이 필요없어서 작은 질량의 먼지도 사용할 수 있고, 길쭉하게 생긴 입자를 사용한다면 연료의 연소 속도를 조절할 수 있고 가속에도 유리함.

DT 연료는 kg 당 330 TJ의 에너지를 가지므로 100 km/s 로 가속한다면 66000배의 에너지를 얻을 수 있고 25960km/s 까지 에너지를 얻을 수 있음.

위에서 예시로 든 밀리미터 크기의 다이아몬드 껍데기는 78마이크로그램의 연료를 담을 수 있고, 껍질 자체 무게의 44배 정도임. 입자의 가속력은 줄어들겠지만, 줄어든 가속력으로도 blowpipe 가속기는 31cm만에 100km/s까지 속도를 올릴 수 있음.
1MW 가속기는 이런 입자 2500개를 발사할수 있을 것이고 64GW의 에너지를 얻을 수 있음.
추진

생각해볼 수 있는 가장 쉬운 용도는 우주선 추진에 사용하는 것임.
작고 가벼운 먼지들은 10000km/s 이상으로 가속할 수 있음. ISP로 환산하면 대략 1000000초에 달함. 강력한 전기추진 엔진이나 가능한 수치이고 핵융합 추진 우주선 정도만이 겨우 넘길 수 있음.
초고속 먼지들은 방사성 물질을 내뿜지도 않고 평벙한 먼지처럼 생겼음. 이 먼지들은 태양광이나 폐쇄형 원자로로(핵연료가 외부로 노출되지 않는 현재 쓰는 방식의 원자로) 가동될 수 있음. 이런 입자들의 흐름은 효율적인 추진 방식으로 고려되어왔고, 항성간 탐사를 가능하게 해줄 수 있을 것임.
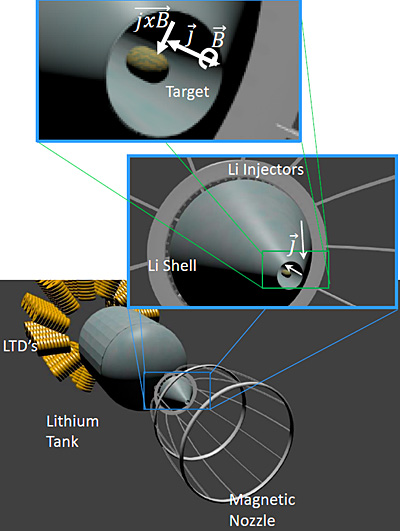
증폭된 핵분열을 추진에 이용할 수도 있음. 우라늄의 임계 질량을 줄여서 펄스 당 에너지를 최소화할 수 있음. 오리온 핵 펄스 우주선에 사용된 핵폭탄은 한 번의 펄스가 627GJ의 에너지를 방출하고 이보다 더 작은 펄스는 우라늄이 불완전 연소하면서 낭비됨. Mag-Orion 이라는 Z-Pinch 버전은 큐륨-245를 사용해서 340GJ의 펄스 에너지를 갖지만, 먼지 가속기를 사용하면 0.04g의 우라늄만으로도 3.2GJ를 낼 수 있음.

핵융합 로켓 또한 미세 입자 가속기로 많은 이득을 얻을 수 있음. 이온 빔이나 레이저로 에너지를 집중해서 핵융합 반응을 일으키는 것처럼, 운동 에너지로도 에너지를 집중할 수 있음. 핵융합 반응을 점화하는 데 필요한 엄청난 에너지는 에너지를 수천 배 이상 덜 소모하는 먼지 가속기로 대체할 수 있음. 먼지들은 우주 공간에서 속도가 감소하지 않으므로 우주선의 바로 뒤에서 핵융합 반응이 점화될 수도 있고 100m의 거리에서도 점화될 수 있음. 이 점은 테라와트급의 torchship 엔진을 만들 때 유용함.(테라와트 급의 엔진은 엄청난 열을 발생시키기 때문에 되도록 먼 거리에서 엔진이 작동해야 면적 당 받는 열을 줄일 수 있음.)
미세 입자들은 우주에서 먼 거리를 빠르게 이동할 수 있고, 운동 에너지를 손실 없이 전달할 수 있음. 여러 묶음의 먼지를 조금씩 다른 속력으로 발사하고 동시에 도착하도록 해서 더 높은 최대 출력을 얻을 수도 있음. 입자를 수신하는 우주선은 입자가 충돌해서 플라즈마 폭발이 일어나게 장애물을 설치해주기만 하면 됨. 그렇게 발생한 플라즈마는 자기 노즐을 통해 분사하면 추진력으로 변환됨. 100km/s의 탄소 먼지를 기화시키기 위한 에너지는 탄소 먼지의 운동 에너지보다 83배 낮으므로 1kg 의 물체로도 83kg의 탄소 먼지를 막을 수 있음.
이런 종류의 추진 시스템은 레이저 세일과 비슷한 점이 많음. 무거운 원자로가 없어도 추진력을 낼 수 있어서 가속이 쉽고 먼지들을 기화시키기 위한 물체 대 먼지의 질량 비가 낮으므로 높은 ISP를 기대해볼 수 있음.
핵분열이나 핵융합을 일으키는 먼지를 사용할 수도 있음.
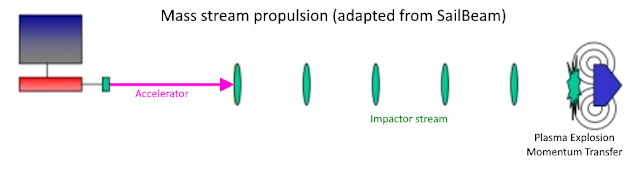
증폭된 핵분열을 일으키는 먼지들은 자기 노즐 내부에 있는 먼지들과 충돌하면서 핵폭발을 일으키고 10000km/s 가 넘는 핵분열 생성물을 배출함. 10kg/s 의 질량 흐름은 80TW의 에너지를 내놓을 것임. 만약 100kg 의 먼지를 받아내는 데 1kg의 장애물이 필요하다면 1000톤 질량 중에서 200톤의 장애물로 된 우주선은 평균 1.81g 로 가속하는 35700km/s dV의 우주선이 될 것임.
만약 50GW 가속기로 핵분열 입자를 가속한다면 이 가속기는 80TW출력을 1000톤짜리 우주선에 전달할 수 있고 이 우주선을 목성까지 9.8~14.5 시간 안에 보낼 수 있음.
레이저나 입자빔을 이용해서 먼지들을 기화시켜서 직접 충돌시키는 대신 전자기장에 충돌하는 방식을 선택할 수도 있음.
레이저는 이 먼지들을 유도하는 데 사용할 수 있음. 먼지들은 레이저에 의해 발생한 전기장 속에서 빔의 중앙에 놓이거나 특이한 각도로 휠 수 있음.
무기로의 사용
초고속 먼지는 무기로 사용될 수 있음.
먼지 가속기는 레이저나 입자 빔에 비해 더 무게가 많이 나가고, 질량 대비 출력도 작으며, 속도도 광속에 미치지 못해 단점만 있는 것처럼 보일 수 있음.
그러나 자세히 보면 장점이 있음.
먼지의 명중 확률은 다음과 같이 나타낼 수 있음.
명중률 = (표적 지름 / (0.5 * 표적 가속력 * (거리/먼지의 속도) ^ 2))^2
이 방정식은 먼지를 목표를 향해 조준(정확히는 표적의 가속력을 고려한 원 모양의 예상 궤적 집합 안에 랜덤으로 발사할 때)할 때 표적이 도망칠 수 있는 영역을 표적의 면적으로 나눈 값임.
2000km 거리에서 0.5g 로 가속하는 우주선을 1000km/s 먼지 가속기로 조준한다면 명중 확률은 30%임.

이 식을 뒤집으면 유효 사거리를 구할 수 있음.
유효 사거리 = 먼지 속도 * 표적 지름^0.5 / (명중률 ^ 0.25 * (0.5 * 표적 가속력) ^ 0.5))
만약 1000km/s 의 먼지 가속기가 명중률 10% 까지 허용한다면, 5m 반지름의 0.5g 가속력을 낼 수 있는 표적의 사거리는 2650km임. 식을 보면 유효 사거리는 먼지의 속도에 비례하지만, 표적의 가속력에는 0.5제곱만큼 반비례함. 또, 2배의 가속도는 4배의 연료를 소모하고, 연료량 또한 무게를 증가하는 요인이므로 우주선은 더 많은 연료와 추력을 요구받게됨.
먼지의 속력이 빨라질수록 유효 사거리는 점점 늘어남.

작은 먼지들은 운동 에너지를 표적의 장갑에 전달해서 플라즈마 폭발을 일으켜서 장갑에 크레이터가 생김. 크레이터의 부피는 대략 운동 에너지를 물체의 항복 강도의 세 배로 나눈 것으로 어림하면(정확하지 않음) 됨. 흑연같은 경우 운동 에너지를 2.4*10^8J/m^3 으로 나누면 됨. 흑연을 기화시키기 위해서는 이보다 500배 많은 에너지가 필요하고, 이는 먼지 질량빔은 레이저나 입자빔보다 500배 더 효율적이라는 뜻임.
탄소섬유같은 강한 물질은 5배 적은 에너지를 요구하지만, 이는 여전히 파괴적인 수치임.
100MW의 먼지 질량빔은 0.41m^3의 흑연이나 0.03m^3의 탄소 섬유를 매 초 마다 굴착할 수 있음. 만약 먼지 입자들을 핵분열을 일으키게 해서 100배의 에너지를 준다면 40m^3, 3m^3이 될 것임. 관통력은 먼지들이 어느 정도의 분산도로 충돌하느냐에 따라 달라질 것임. 만약 1m 지름의 원 안이라면 관통력은 흑연일 때 51m/s 일 것이고 위에서 본 예제처럼 5m 반지름의 물체에 10% 확률로 명중할 때에는 흑연일 경우 5cm/s, 탄소섬유의 경우 0.38cm/s 임.

작은 물체가 빠른 속도로 날아올 경우 효과적인 장갑인 whipple shield라는 게 있음. 위에서도 말했듯이 먼지가 물체를 파괴할 수 있는 질량은 작지만, 한 번의 충돌 만으로도 whipple shield가 파괴되면서 관통하는 입자의 양은 수천 배 증가함.

한 개의 먼지가 들어오는 건 whipple shield를 한 층 늘리는 것보다 훨씬 쉬움.
먼지 가속기의 공격 능력은 핵분열이나 핵융합 물질을 내부에 탑재했을 때 극대화됨. 먼지 가속기는 소비한 에너지보다 더 많은 에너지를 표적에 방출할 수 있음. 1MW 먼지 가속기는 1MW 레이저나 입자빔보다 무거울 수도 있고 부피가 클 수도 있지만, 목표물에서의 출력은 100배에서 1000배까지 증가할 수 있음.
먼지를 탐지하는 것 또한 매우 어려울 것임. 크기가 작고 표면적이 넓기 때문에 배경 복사와 구분이 어렵고 라이다조차 제대로 반응할 수 없음. 짧은 파장의 라이다를 사용한다면 탐지할 수도 있겠지만, 해상도가 심각하게 제한될 것임.(파장이 짧은데 왜 해상도인지 모르겠음 거리 아닌가?) 만약 탐지했다 해도 격추하기 어려움. 레이저로도 몇 초밖에 대응할 수 없고, 먼지들은 표면적이 넓기 때문에 쉽게 가열되지도 않음.
예를 들어보자면 마이크로미터 크기의 탄소 섬유는 58MW/m^2에서 살아남을 수 있고 마이크로미터 지름 센티미터 길이 탄소섬유 바늘은 579GW/m^2에서 살아남을 수 있음. 레이저가 아무리 강력해도 먼지들은 레이저를 뚫고 들어올 수도 있다는 것임.

SDI 시대에 이미 우주 방어용 먼지 가속기가 연구된 적 있음.
번역 출처:
http://toughsf.blogspot.com/2019/11/hypervelocity-macron-accelerators.html
의역이나 오역 있을 수 있고 몇몇 난잡한 문장은 빠졌을 수도 있음.
'Space > 하드SF' 카테고리의 다른 글
| 다른 행성에서 사는 법: 천왕성 (0) | 2023.03.28 |
|---|---|
| 다른 행성에서 살아남기: 수성 (0) | 2023.02.19 |
| 핵 펄스 추진 기술의 기계화 (0) | 2022.10.19 |
| 핵분열 물질 없는 핵융합 (0) | 2022.10.19 |
| 핵 성형작약 (0) | 2022.02.20 |




댓글