라플라스 방정식 -직각좌표계

라플라스방정식의 전산적 풀이

전에 라플라스 방정식을 전산적으로 푸는 방법을 소개했다. 오늘은 라플라스 방정식을 해석적으로 풀어보자

라플라스 방정식을 모른다면 위의 글을 읽어보고 오자(코드 부분은 안봐도 된다.)

 

티스토리 앱이나 몇몇 브라우저에저에서 수식이 안 보일 수 있다. 댓글 부탁한다.

 

 

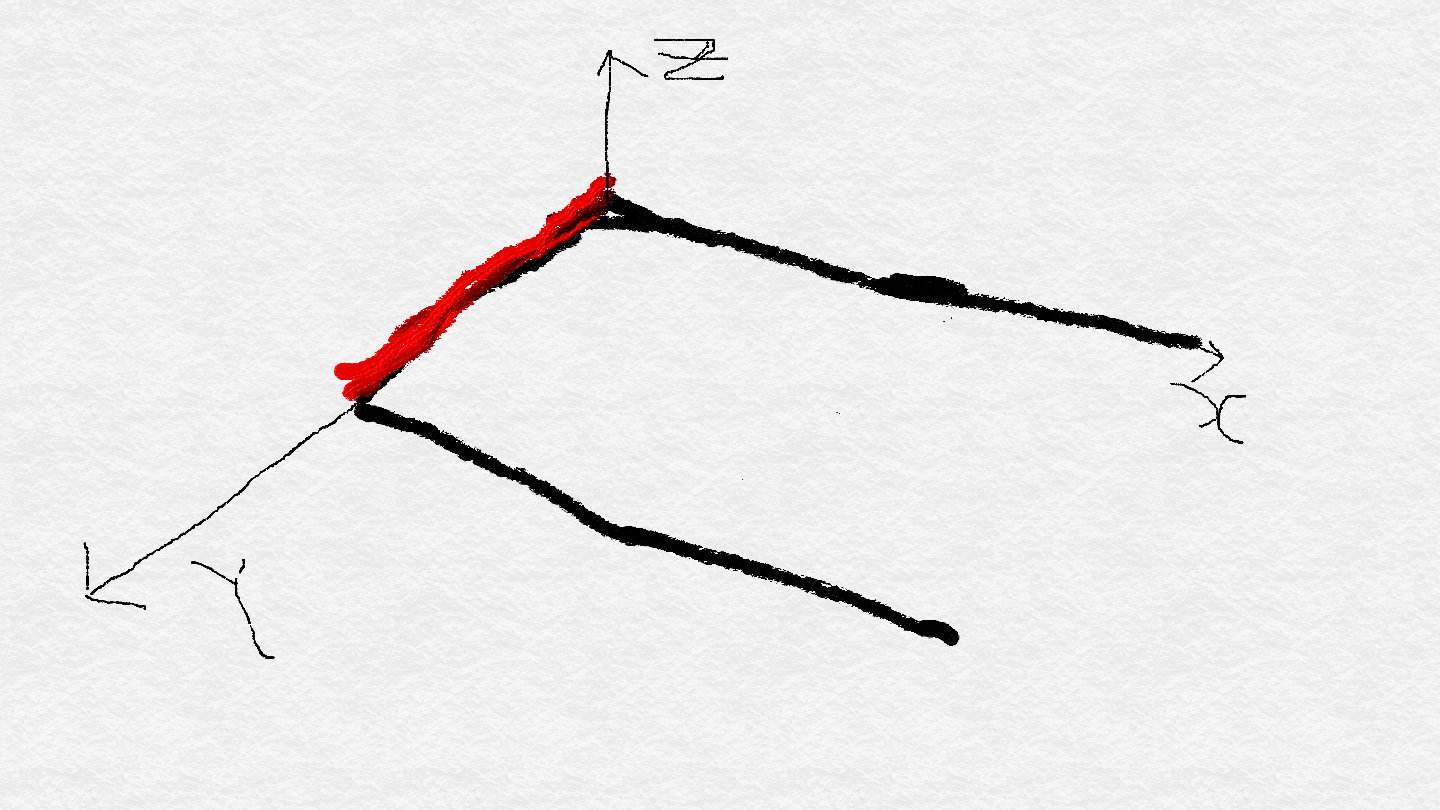
이런 경계조건($x = 0$의 전위가 $V_0$일 때)이 있다고 하자

그럼

$\triangledown^2V = 0$

이런 식이 만족된다.

 

즉

$\frac{\partial ^2V }{\partial x^2} + \frac{\partial ^2 V}{\partial y^2} = 0$

이 식을 위에서의 경계 조건에 맞게 풀어야 한다.

 

경계조건:

1) $y = 0$ 일 때 $V = 0$

2) $y = a$ 일 때 $V = 0$

3) $x = 0$ 일 때 $V = V_0(y)$

4) $x \rightarrow \infty$ 일 때 $V \rightarrow 0$

 

일단 이 방정식을 풀기 위해 $V(x,y) = X(x)Y(y)$ 형태의 해를 시험해보자

 

이 식을 위의 라플라스방정식에 넣으면

$Y\frac{d^2X}{dx^2} + X\frac{d^2Y}{dy^2} = 0$

 

양변에 $V$를 나눠주면

$\frac{1}{X}\frac{d^2X}{dx^2} + \frac{1}{Y}\frac{d^2Y}{dy^2} = 0$

 

이렇게 변수가 각 항에 분리된다.(이 방법을 변수분리법이라 한다. 꽤나 Ad Hoc스럽기도 하지만 미분방정식이 다 그렇지 뭐)

어쨌든 이 식은 $f(x)+g(y)=0$ 이렇게 쓸 수 있다. $f(x)$ 와 $g(x)$는 모두 상수여야 할 것이다.

 

그러면

$\frac{1}{X}\frac{d^2X}{dx^2} = C_1$, $\frac{1}{Y}\frac{d^2Y}{dy^2} = C_2$

라고 쓸 수 있다.($C_1 = -C_2$)

 

그럼 $C_1$을 양수 $k^2$, $C_2$를 음수$-k^2$라고 놓고 풀어보자

 

$\frac{d^2X}{dx^2} = k^2 X$, $\frac{d^2Y}{dy^2} = -k^2 Y$

그럼 이 미분방정식 2개를 풀면.

 

$X(x) = Ae^{kx} + Be^{-kx}$, $Y(y) = C\sin(ky)+D\cos(ky)$

아까 $V(x,y) = X(x)Y(y)$ 라고 했으므로

 

$V(x,y) = (Ae^{kx} + Be^{-kx})(C\sin(ky)+D\cos(ky))$

근데 초기조건 4에서 $x \rightarrow \infty$ 일 때 $V \rightarrow 0$이므로 A가 0이어야 전위가 무한대로 가지 않는다.

 

초기조건 1때문에 $y=0$에서 V의 값이 0이어야 하므로 D는 0이다.

초기조건 2때문에 $y=a$에서 V의 값이 0이어야 하므로 $\sin ka = 0, k=\frac{n\pi}{a}, (n = 1,2,3,...)$이다.

 

따라서 일단은 라플라스방정식의 해는

$V(x,y)  = Ce^{-kx} \sin(\frac{n\pi}{a}y)$

이다.

 

근데, 이 때 라플라스방정식의 해는 아주 많다.(n값마다 한개의 해가 존재한다.)

라플라스방정식은 선형성을 가지므로 서로 더할 수 있는데(선형: 교환법칙, 결합법칙 성립) 각각의 n값에 대해 가지는 해를 모두 더하면 하나의 해를 구할 수 있다. ex) $\triangledown^2 V = a_1\triangledown^2 V_1+a_2\triangledown^2 V_2+a_3\triangledown^2 V_3... = 0$

 

따라서 해를 다시쓰면

$V(x,y) = \sum_{n=1}^\infty C_n e^{-n\pi x/a} \sin{n\pi y/a}$

 

$x=0$일 때 $V(y)$도 0이므로

$V(0,y) = \sum_{n=1}^\infty C_n \sin{n\pi y/a} = V_0(y)$

이걸 푸리에 적분하면

 

$\sum_{n=1}^\infty C_n \int_0^a \sin(n\pi y /a) \sin(n\prime \pi y /a)dy = \int_0^a V_0(y) \sin(n\prime \pi y /a) dy$

인데,

 

$\int_0^a \sin(n\pi y /a) \sin(n\prime \pi y /a)dy$가 직교하면($n \neq n\prime$) 0, 직교하지 않으면 ($n = n\prime$) 1/2이므로 $n = n\prime$인 항만 남는다.

 

$C_n$을 구하면

$C_n = \frac{2V_0}{a}\int_0^a \sin(n\prime \pi y /a) dy = \frac{2V_0}{n\pi}(1-\cos n\pi)$

이고,

$C_n$은 n이 홀수일 때 0이고, 짝수일 때 $\frac{4V_0}{n\pi}$의 값을 갖는다.

 

정리하면 이 방정식의 해는

$V(x,y) = \frac{4V_0}{\pi} \sum_{n=1,3,5...} \frac{1}{n} e^{-n \pi x/a} \sin(n \pi y /a)$

이다.

 

 

아까 라플라스 방정식은 선형성을 가진다고 했는데, 경계조건이 다른 라플라스방정식의 해끼리 더하면, 경계조건을 합친 것의 해와 같다.

 

그러니까

 

 

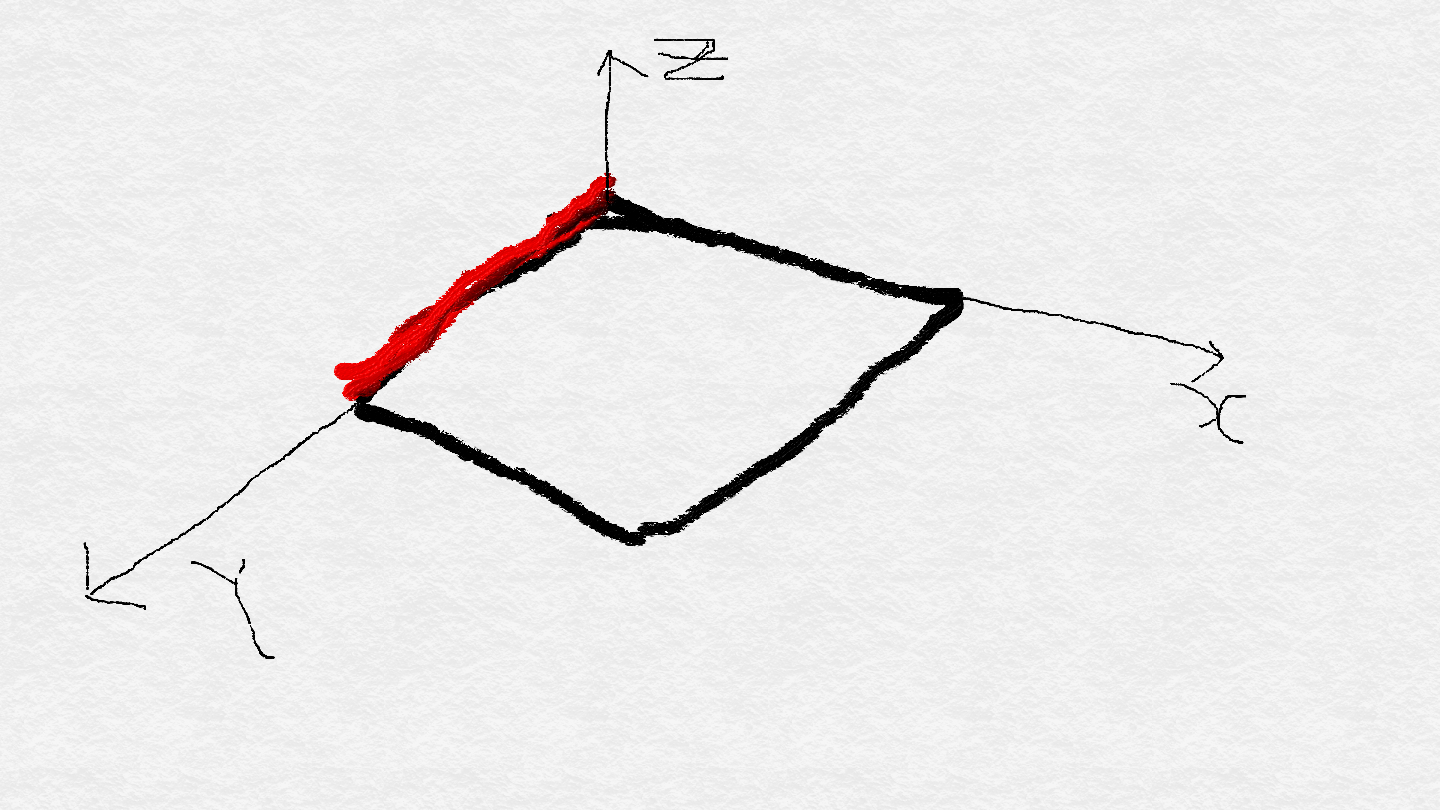
이거 더하기

 

 

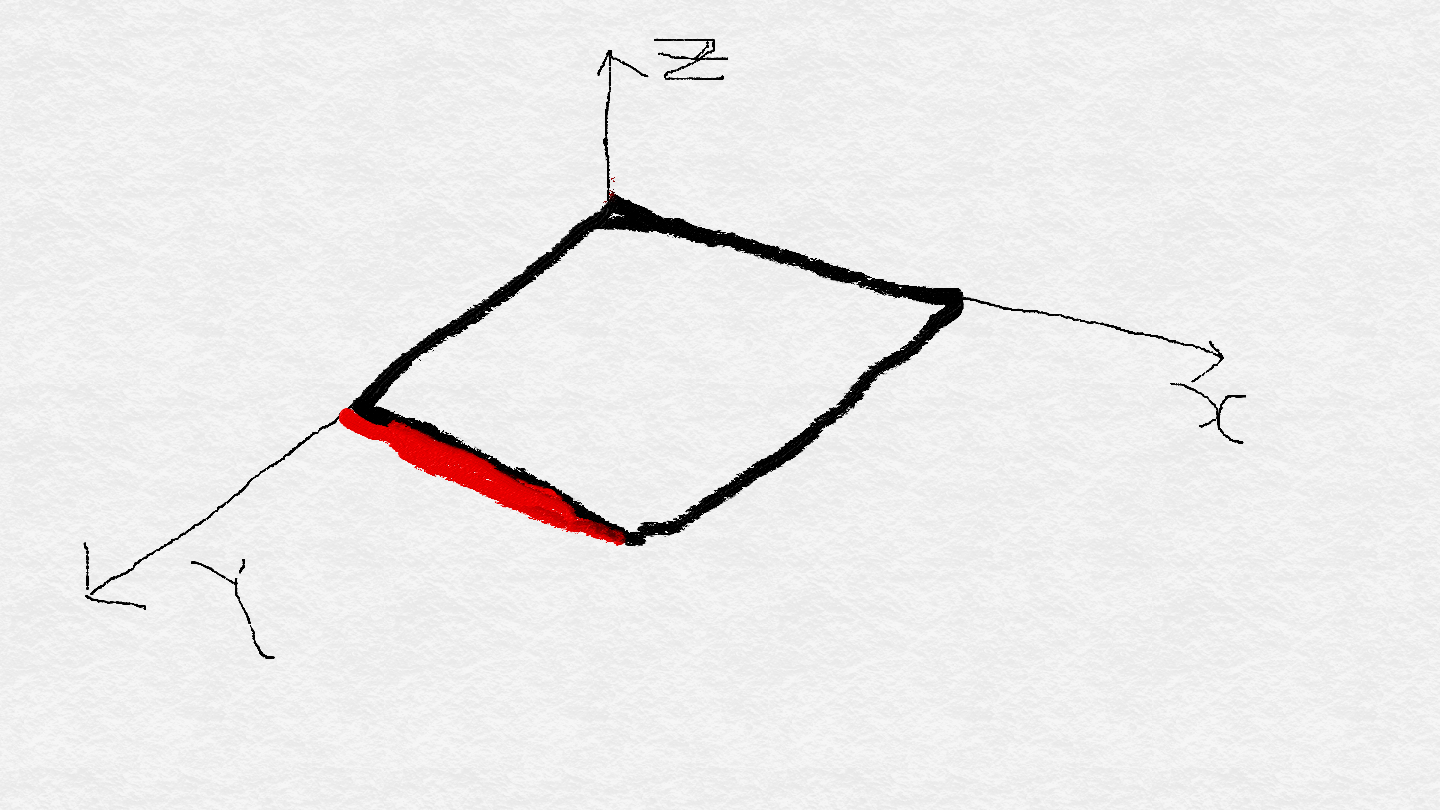
이거는

 

 

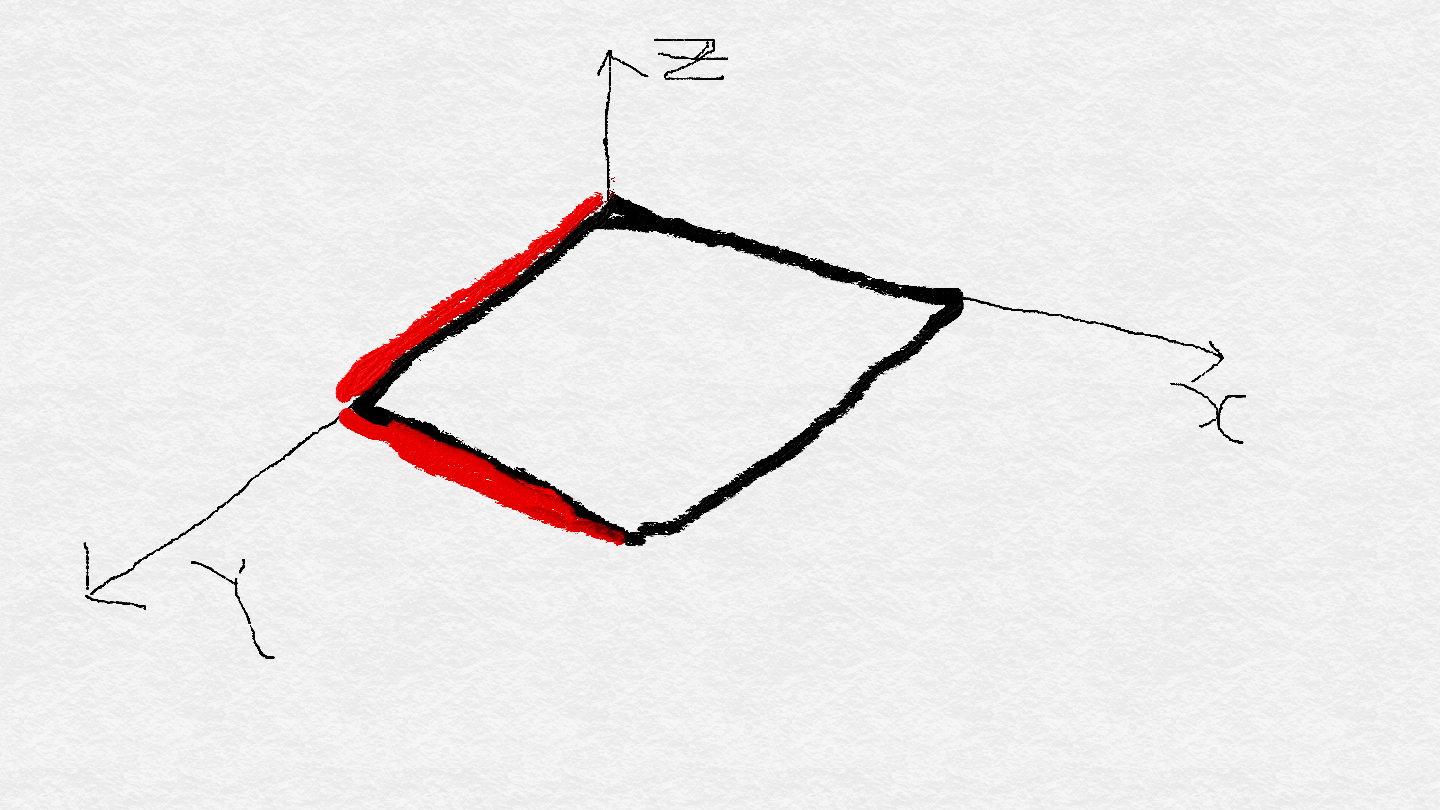
이거 해랑 같다는 것이다.

 

 

 

라플라스방정식은 전자기학에서 전위를 구할 때 쓰인다.

구좌표계나 원통좌표계에서 전개하는 것은 르장드르 다항식을 써야 하기 때문에 나중에 하겠다.

 

+매스매티카에서 풀어봤는데, 시간아 아주 오래 걸린다. 그럴 만 한 거긴 하지만...